The radii of the two columne is U-tube are r1 and r2(>r1). When a liquid of density ρ (angle of contact is 0∘)) is filled in it, the level different of liquid in two arms is h. The surface tension of liquid is
(g= acceleration due to gravity)
ρghr1r22(r2−r1)
ρgh(r2−r1)2r1r2
2(r2−r1)ρghr1r2
ρgh2(r2−r1)
The correct Answer is:A
Here, h1=2Scos0∘r1ρgandh2=2Scos0∘r2ρg
∴h1−h2=2Scos0∘ρg[1r1−1r2]=2S(r2−r1)r1r2ρg
But h1−h2=h (given)
∴h=(2S(r2−r1))r1r2ρgorS=r1r2hρg2(r2−r1)
Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBook:MTG GUIDEChapter:PROPERTIES OF BULK MATTERExercise:Check Your Neet Vitals
Explore 22 Videos
- PROPERTIES OF BULK MATTERBook:MTG GUIDEChapter:PROPERTIES OF BULK MATTERExercise:AIPMT/NEET (MCQs)
Explore 40 Videos
- PROPERTIES OF BULK MATTERBook:MTG GUIDEChapter:PROPERTIES OF BULK MATTERExercise:AIPMT/NEET (MCQs)
Explore 40 Videos
- PHYSICAL WORLD AND MEASUREMENTBook:MTG GUIDEChapter:PHYSICAL WORLD AND MEASUREMENTExercise:AIPMT / NEET MCQ
Explore 14 Videos
- THERMODYNAMICSBook:MTG GUIDEChapter:THERMODYNAMICSExercise:AIPMT/NEET (MCQs)
Explore 26 Videos
Similar Questions
The radii of two columns in a U tube are r1andr2(r1>r2). A liquid of density ρ is filled in it. The contact angle of the liquid with the tube wall is θ. If the surface tension of the liquid is T then plot the graph of the level difference (h) of the liquid in the two arms versus contact angle θ. Plot the graph for angle θ changing from 0∘→90∘. Assume the curved surface of meniscus to be part of a sphere.

View SolutionIn a U-tube the radii of two columns are respectively r1andr2 and if a liquid of density d filled in it has level difference of h then the surface tension of the liquid is -
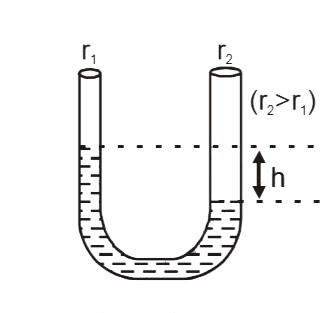
View Solution
Knowledge Check
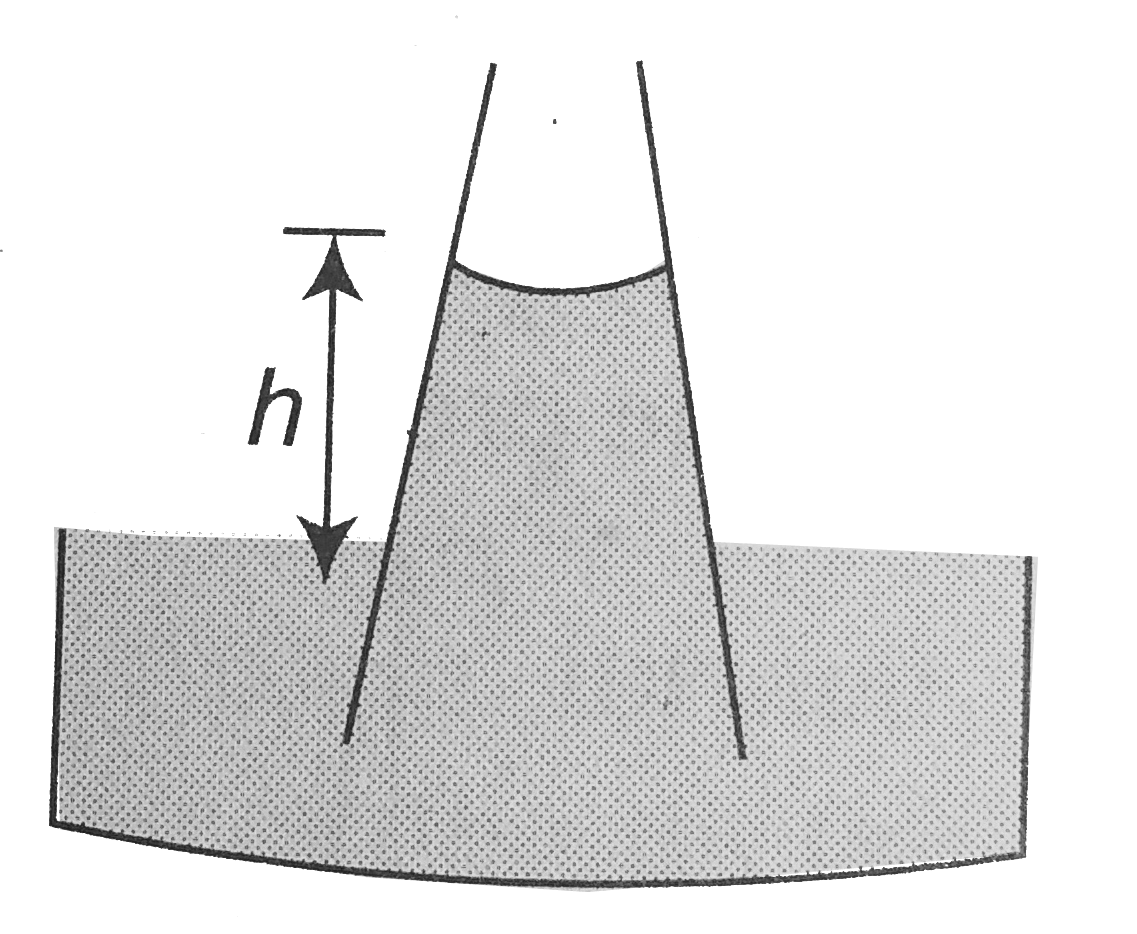
A capillary of the shape as shown is dipped in a liquid. Contact angle between the liquid and the capillary is 0∘ and effect of liquid inside the mexiscus is to be neglected. T is surface tension of the liquid, r is radius of the meniscus, g is acceleration due to gravity and ρ is density of the liquid then height h in equilibrium is:Agreater than 2TrρgBequal to 2TrρgCless than 2TrρgDof any value depending upon act.A beaker containing a liquid of density ρ moves up with an acceleration a. The pressure due to the liquid at a depth h below the free surface of the liquid is.
AhρgBhρ(g+a)Chρ(g−a)D2hρg(g−ag+a)If h is the rise of water in a capillary tube of radius r, then the work done by the force of surface tension is
(ρ is density g = (acc)n due to gravity )A2gT2ρπB2πT2ρgC4gT2ρπD4πT2ρg
A container having a liquid of density ρ is moving downwards with acceleration g2. Find the pressure difference between two vertical points in the liquid separated by h
View SolutionStatement-1: The angle of contact of a liquid decrease with increase in temeperature
Statement-2: With increase in temperature the surface tension of liquid increase.
View SolutionA capillary tube of radius r is lowered into a liquid of surface tension T and density ρ. Given angle of contact =0∘.
What is the potential energy acquired by the liquid in the capillary?
View SolutionTwo holes are made at depths h and 2h from the top. A liquid of density ρ and height h is filled over another liquid of density 2ρ. Speeds of liquid ejecting from two holes are say v1 and v2.

If density of lower liquid is increased
View SolutionThe absolute pressure at a depth h below the surface of a liquid of density ρ is [Given Pa = atmospheric pressure, g = acceleration due to gravity]
View Solution

