Question

Derive the formula for the electric potential energy of system of two charges.

Explanation

Consider the charges `q_(1)` and `q_(2)` initially at infinity. Suppose, first the charge `q_(1)` is brought from infinity to the point by distance `r_(1)`. There is no extermal field against which work needs to be done, so work done in bringing `q_(1)` from infinity by distancer `r_(1)` is,
`:. W_(1)=0`

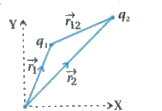
This charge `q_(1)` produces a potential in space is `V_(1)= (kq_(1))/(r_(1)p)`
where `r_(1)p` is the distance of a point P in space from the location of `q_(1)` .
Now work done in bringing charge `q_(2)` from infinity to the given point by distance `r_(2)` in the electric field of `q_(1)` is
`W_(2)=q_(2)V_(1)`
`:. W_(2)=(kq_(1)q_(2))/(r_(12))`
where `r_(12)` is the distance between points 1 and 2 at distance `r_(1)` and `r_(2)` .
Since electrostatic force is conservative this work gets stored in the form of potential energy of the system.
Potential energy of system of two charges `q_(1)` and `q_(2)` is,
`U= W_(1)+W_(2)`
`:. U= (kq_(1)q_(2))/(r_(12))`
If `q_(2)` was brought first to its present location and `q_(1)` brought later the potential energy would be according to equation (2).
Generally, the potential energy expression is unaltered whatever way the charges are brought to the specified locations because the path independence of work for electrostatic force.
`:. U=k[0+(q_(1)q_(2))/(r_(12))+(q_(1)q_(3))/(r_(13))+(q_(2)q_(3))/(r_(23))]`
`:. U=k[(q_(1)q_(2))/(r_(12))+(q_(1)q_(3))/(r_(13))+(q_(2)q_(3))/(r_(23))]`
Equation (2) is true for any sign of `q_(1)`, and `q_(2)`.
If `q_(1) q_(2) gt0` potential energy will be negative.
And if `q_(1)q_(2) lt 0` potential energy will be negative .