Question

Define electrostatic potential energy. Derive an expression for it due to a system of two charges.

Explanation

Electrostatic potential energy Electrostatic potential energy of a system of point charges is defined as the total amount of work done in bringing the different charges to their respective positions from infinitely large mutual separations.
Electrostatic Potential Energy of a System of Two Point Charges
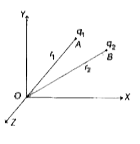
Consider two point charges `q_(1) and q_(2)` lying at points A and B, whose locations are `r_(1) and r_(2)` respectively. To find the electric potential energy of this two charge system, we must mentally build the system, starting with both charges infinitely far away and at rest. First, the charge `q_(1)` is brought from infinity to the point `r_(1)`. There is no external field against which work needs to be done, so work done in bringing `q_(1)` from infinity to `r_(1)` is zero. V is potential that has been set up by `q_(1)` at the point B, where `q_(2)` is to be placed `therefore V= (1)/(4pi epsi_(0)).(q_(1))/(r_(AB))`
where `r_(AB)` is the distance between points A and B. By definition, work done in carrying charge `q_(2)` from `oo` to B.
W = Potential `xx` Charge
`W = (1)/(4pi epsi_(0)) (q_(1))/(r_(AB)) .q_(2)= (1)/(4pi epsi_(0)).(q_(1)q_(2))/(r_(AB))`
This work is stored in the system of two point charges `q_(1) and q_(2)` in the form of electrostatic potential energy U of the system.
Thus , `U= W= (1)/(4pi epsi_(0)).(q_(1)q_(2))/(r_(AB))`
Electrostatic potential energy is a scalar quantity. In the above formula, the values of `q_(1) and q_(2)` must be put with proper signs.
If `q_(1) q_(2) gt 0`, then potential energy is positive. It means that two charges are of same sign i.e., they repel each other. If `q_(1) gt 0, q_(2) lt 0` then potential energy is negative. It means that two charges are of opposite sign, i.e., they attract each other.