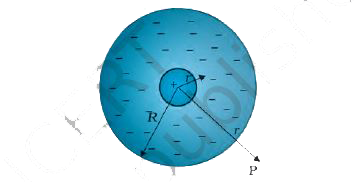
An early model for an atom considered it to have a positively charged point nucleus of charge Ze, surrounded by a uniform density of negative charge up to a radius R. The atom as a whole is neutral. For this model, what is the electric field at a distance r from the nucleus ?
Solution in Gujrati

Video Solution

Text Solution

Verified by Experts

Here, nucleus of atom of an element with atomic no. Z has total positive charge + Ze (where + e is the charge of one proton) surrounding to this central positive point charge, uniform volume distribution of equal negative charge was considered up to radius R, as per the early model of neutral atom.
If volume charge density of this negative charge is $ρ$ then,
$ρ = \frac{total negative charge in an atom}{volume of spherical atom}$
$∴ ρ = \frac{- Z e}{\frac{4}{3} π R^{3}} = - \frac{3 Z e}{4 π R^{3}}$ .............(1)
Now let us find out electric field for following three cases.
(i) For $r_{i} < R$ (inside the atom)
Consider spherical Gaussian surface with radius $r_{i}$ and surface area $4 π r_{i}^{2}$ . Magnitude of electric field at any point on this surface is same because of spherical symmetry. Let it be $E_{i}$ ,
Here net charge enclosed by above Gaussian surface is,
$q = Z e + \frac{4}{3} π r_{i}^{3} ρ$
$= Z e + \frac{4}{3} π r_{i}^{3} (- \frac{3 Z e}{4 π R^{3}})$ (From equation (1))
$∴ q = Z e (1 - \frac{r_{i}^{3}}{R^{3}})$ .........(2)
Applying Gauss theorem for considered Gaussian surface,
$\int {\vec{E}}_{i} . \vec{d s} = \frac{q}{ε_{0}}$
$∴ \int E_{i} d s {\cos 0}^{\circ} = \frac{Z e}{ε_{0}} (1 - \frac{r_{i}^{3}}{R^{3}}) (∴ {\vec{E}}_{i} ∣ ∣ \vec{d s})$
$∴ E_{i} = \frac{Z e}{4 π ε_{0}} (\frac{1}{r_{i}^{2}} - \frac{r_{i}}{R^{3}})$ ........(3)
Above electric field is directed radialh outward.
(ii) For $r_{0} > R$ (outside the atom)
Consider spherical Gaussian surface witri radius $r_{0}$ and surface area $4 π r_{0}^{2}$ . Magnimde of electric field at any point on this surface! is same because of spherical symmetry. Let it be $E_{0}$
Here, net charge enclosed by above Gaussian surface,
$\int {\vec{E}}_{0} . \vec{d s} = \frac{q}{ε_{0}}$
$∴ E_{0} = 0 (∴ q = 0)$ ...........(4)
(iii) On the surface of atom (r = R)
If we consider spherical Gaussian surface with radius r = R then charge enclosed by it is also q = Ze + (-Ze) = 0 and so electric field on the surface of atom is $E_{s} = 0$ .
From equation (3) also, we get electric field on the surface of atom,
$E_{s} = \frac{Z e}{4 π ε_{0}} (\frac{1}{R^{2}} - \frac{R}{R^{3}})$ (For r=R)
$= \frac{Z e}{4 π ε_{0}} (\frac{1}{R^{2}} - \frac{1}{R^{2}})$
$∴ E_{s} = 0$
Conclusion :
(i) At distance $r_{i} < R$ from the centre of atom, electric field is,
$E_{i} = \frac{Z e}{4 π ε_{0}} (\frac{1}{r_{i}^{2}} - \frac{r_{i}}{R^{3}})$ (Radially outward)
(ii) At distance $r \geq R$ from the centre of atom, electric field is,
$E_{0} = E_{s} = 0$

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

KUMAR PRAKASHAN-ELECTRIC CHARGES AND FIELDS -SECTION B NUMERICALS (NUMERICAL FROM TEXTUAL ILLUSTRATIONS)

Home
Ask Doubt
Profile