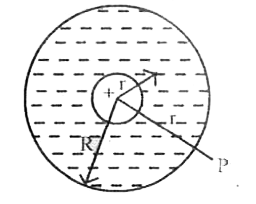
The classical concept of atomic structure is that negative charges are uniformly distributed inside a sphere of radius R keeping the nucleus of positive charge Ze at the centre of that sphere. An atom as a whole is electrically neutral. find out the electric field at a distance r from the nucleus, according do this atomic model. Solution in Bengali
Charge of the nucleus = +Ze
∴ Amount of charge outside the nucleus = −Ze, as an atom is electrically neutral.
Volume density of negative charge inside the sphere,
ρ=−Ze43πR3=−3Ze4πR3
Electric field at external points (r>R) : Let A be any such point outside the sphere . A concentric sphere of radius r, passing through A, is a convenient Gaussaian surface.
The change enclosed by this Gaussian surface,
q = charge of the nucleus + charge distributed inside the sphere of radius R <br> = + Ze+ ( - Ze ) = 0<br> therefore FromGauss'theorem, oint _ S vecE * dvecS = (q ) /( in _ 0 ) = 0 <br> therefore E = 0,atallexternalp∮s.<br>E≤ctricfieldat∫ernalp∮s( r lt R ):LetBbeanysuchp∮∈sthesphere.Aconcentricsphereofradiusr,passingthroughB,isaconvenientGaussiansurface.Itis→be¬edtˆthissuraceenclosestheentirepositivechar≥+ Ze oftheνc≤us,butapartofthe¬ativechar≥ - Ze rema∈soutsit.<br>Theamountof¬ativechar≥∈sthisGaussiansurface,<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/CHY_DMB_PHY_XII_P1_U01_C02_SLV_059_S01.pngwh=80%mx-autosty≤=background:white;><br> q ' =volumeofthisenclosedsphere xx volumedensity rho of¬ativechar≥<br> = ( 4 )/(3) pi r ^ 3 ( - (3 Ze )/( 4pi R ^ 3 ) ) = - Ze ( r^ 3 )/( R ^ 3 ) <br> therefore Netchar≥enclosedbythesphere<br> q = + Ze + q' = Ze - Ze ( r ^ 3 ) /( R ^ 3 ) = Ze ( 1 - ( r ^ 3 )/( R ^ 3 )) <br>Foranysurfacee≤ment d vecS ontheGaussiansurface,thee≤ctricfield vec E andthearea→−−→r d vec S areparal≤l→eachother<br> therefore vec E * d vecS = Ed S cos 0^ @ = EdS <br>Aga∈,omsymmetry,Eisuniform∈magniturdeovertheGaussiansurface.then,omGauss'theorem,<br> oint _ S vec E * d vecS = ( q ) /( in _ 0 ) <br>or, oint_S EdS = (q )/( in _ 0 ) or, E oint _ S dS = ( q )/( in _ 0 ) or, ES = (q ) / ( in _ 0 ) <br>or, E * 4pi r^ 2 = (1 ) /( in _ 0 ) Ze ( 1 - (r ^ 3 )/( R ^ 3 )) <br>or, E = ( Ze )/( 4pi in _ 0) * ( 1 ) /( r ^ 2 ) ( 1 - (r^ 3 )/( R ^ 3 ) ) = ( Ze ) /( 4pi in _ 0) (( 1 )/( r^ 2 ) - ( r) /( R ^ 3 ))
Topper's Solved these Questions
- ELECTRIC FIELDBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC FIELDEXERCISE - SECTION RELATION QUESTIONS
50 Videos
- ELECTRIC FIELDBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC FIELDEXERCISE - HIGHER ORDER THINKING SKILL QUESTIONS
33 Videos
- ELECTRIC ENERGY AND POWERBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC ENERGY AND POWEREXERCISE - CBSE SCANNER
7 Videos
- ELECTRIC POTENTIAL BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC POTENTIAL EXERCISE - CBSE Scanner
13 Videos
Similar Questions
State Coulomb's law regarding the force of interaction between two point charge. Define the unit of charge from this law.
View SolutionTwo charges, +qand−q are separated by a distance d. At which points will the resultant electric field intensity be directed parallel to the line joining the charges ?
View SolutionA light bulb is rated 100 W for 220 V ac supply of 50 Hz. Calculate
the resistance of the bulb ,
View SolutionA test charge q is moved without acceleration along the path from A to B from B to C in electric field E as shown in fig.

(i) Calculate the potential difference between A and C.
View SolutionAccording to early model of an atom, the atom is considered it to have a positively charged point nucleus of charge Ze surrounded by a uniform density of negative charge up to a radius R. The atom as a whole is neutral. The electric field at a distance r from the nucleus is (r<R)

View SolutionAccording to Thomson's model, every atom consists of a positively charged sphere of radius 10−10m in which entire mass and positive charge of the atom are uniformly distributed. Inside the sphere, electrons are embedded like seeds in a watermelon. According Rutherford, entire positive charge and mass of the atom are concentrated in a tiny central core of the atom, which is called atomic nucleus. Size of nucleus ≈10−15m. The nucleus contains proton and neutrons. Negatively charged electrons revolve around the nucleus in circular orbits.
The size of atom is of the order of
View SolutionA charge Q is uniformly distributed inside a non- conducting sphere of radius R . Find the electric potential energy stored in the system.
View SolutionA solid sphere of radius R has a spherical cavity of radius r as shown in the figure. If the volume charge density sigma is uniformly distributed over the whole volume of the sphere, then electric field strength at the centre of the sphere will be
View Solutionप्रारम्भ में परमाणु के मॉडल (atomic model) के लिए यह माना गया था कि प्रत्येक परमाणु +Ze आवेशयुक्त एक बिन्दुवत नाभिक (nucleus) होता है जो R त्रिज्या के गोले (sphere) तक उसी परिमाण के ऋण आवेश से एकसमान रूप से (uniformly) घिरा है ताकि परमाणु पूर्णरुमेण उदासीन (neutral) हो। इस मॉडल के लिए नाभिक से r दूरी पर विधुत-क्षेत्र ज्ञात करें, यदि (i) r>R तथा (ii) r<R
View SolutionAccording to early model of an atom,the atom is considered it to have a positively charged point nucleus of charge Ze surrounded by a uniform density of negative charge up to a radius R. The atom as a whole is neutral. The electric field at a distancer from the nucleus is (r<R)

View SolutionConsider an atom with atomic number Z as consisting of a positive point charge at the centre and surrounded by a distribution of negative electricity uniformly distributed within a sphere of radius R. The electric field at a point inside the atom at a distance r from the centre is
View Solutionपरमाणु के प्रारंभिक प्रतिरूप में यह माना गया था कि आवेश Ze का बिंदु आमाप का घनात्मक नाभिक होता है जो त्रिज्या तक एकसमान घनत्व के ऋणावेश से घिरा हुआ है। परमाणु पूर्ण रूप में विधुत उदासीन है। इस प्रतिरूप के नाभिक से r दूरी पर विधुत क्षेत्र कितना है ?
View SolutionAn early model for an atom considered to have a positively charged point nucleus of charge Ze surrounded by a uniform density of negative charge up to a radius R. The atom as a whole is neutral. For this model, what is the electric field a distance r from the nucleus, where r>R ?
View SolutionAn atom was earlier assumed to be sphere of radius a having a positively charged point nucleus of charge +Ze at its centre . This nucleus was believed to be surrounded by a uniform desity of negative charge that made the atom neutral as a whole.
Use this theorem to find the electric field of this atom at a distance r(r>a) from the centre of the atom.
View SolutionAccording to early model of an atom,the atom is considered it to have a positively charged point nucleus of charge Ze surrounded by a uniform density of negative charge up to a radius R. The atom as a whole is neutral. The electric field at a distancer from the nucleus is (r<R)

View Solution
