A rectangular loop of wire ABCD is kept close to an infinitely long wire carrying a current I(t)=I0(1−tT) for 0≤t≤T and I(0)=0 for t > T as shown in figure. Find the total charge passing through a given point in the loop, in time T. The resistance of the loop is R.
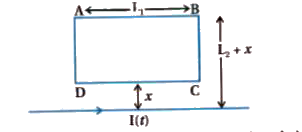 Solution in Gujrati
Solution in Gujrati
Considering strip of thickness dr and length I at distance r from very long current carrying wire.
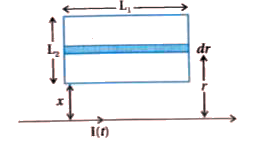
Magnetic flux linked with this strip,
dϕ=BA=μ0I2πr(L1dr)
dϕ=μ0IL12πrdr
Net flux linked with whole loop ABCD,
ϕ=∫L2+xxμ0IL12πrdr
=μ0IL12π[lnr]L2+xx
ϕ=μ0IL12πln(L2+xx)
I(t)=I0(1−tT)
∴ϕ=μ0L12πI0(1−tT)ln(L2+xx)
Now induced charge,
Q=ΔϕR
Q=ϕ1−ϕ2R
For t=0 flux
ϕ1=μ0L12πI0(1−0)ln(L2+xx)=μ0L1I2πln(L2+xx)
For t=T time flux ,
ϕ2=μ0L12πI0(0)ln(L2+xx)=0
⇒Q=ΔϕR=μ0L1I02πRln(L2+xx)
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:KUMAR PRAKASHANChapter:ELECTROMAGNETIC INDUCTIONExercise:Section D MCQs (From DARPAN Based on Textbook )
Explore 121 Videos
- ELECTROMAGNETIC INDUCTIONBook:KUMAR PRAKASHANChapter:ELECTROMAGNETIC INDUCTIONExercise:Section D MCQs (MCQs asked in Competitive Exams )
Explore 38 Videos
- ELECTROMAGNETIC INDUCTIONBook:KUMAR PRAKASHANChapter:ELECTROMAGNETIC INDUCTIONExercise:Section C Ncert Exemplar Solution (Short Answer )
Explore 5 Videos
- ELECTRIC CHARGES AND FIELDS Book:KUMAR PRAKASHANChapter:ELECTRIC CHARGES AND FIELDS Exercise:SECTION D MCQS ASKED IN COMPETITIVE EXAMES (MCQS AKSED IN BOARD EXAM AND GUJCET)
Explore 14 Videos
- ELECTROMAGNETIC WAVESBook:KUMAR PRAKASHANChapter:ELECTROMAGNETIC WAVESExercise:BOARD.S QUESTION PAPER MARCH - 2020 (PART - B) SECTION - C
Explore 5 Videos
Similar Questions
When a metallic rod falls freely, keeping its length horizontal and parallel to north-south direction, emf induced across it is ______
View SolutionThree pure inductance each of 3 H are connected as shown in figure. The equivalent inductance of this connection between points A and B is ......

View SolutionA magnetic field in a certain region is given by →B=B0cos(ωt)ˆk and a coil of radius a with resistance R is placed in the xy-plane with its centre at the origin in the magnetic field (see figure). Find the magnitude and the direction of the current at (a, 0, 0) at t=π2ω,πω and t=3π2ω.
View SolutionWhen air is replaced by dielectric medium of constant K, the maximum force of attraction between two charges separated by distance d, ..........
View SolutionDetermine the current in each branch of the given network.

View SolutionIn Fig. there is a conducting loop ABCDEF of resistance lambda per unit length placed near a long straight current-carrying wire. The dimension are shows in the figure. The long wire lies in the plane of the loop. The current in the long wire varies as I = I_(0)(t) . The heat produced in the loop in time t is
View SolutionA stationary circular loop of radius a is located in a magnetic field which varies with time from t=0→t=T according to law B=B0t(T−t). If plane of loop is normal to the direction of field and resistance of the loop is R, calculate
amount of heat generated in the loop during this interval.
View SolutionConsider an infinitely long wire carrying a current I (t),
With dIdt=λ = constant . Find the current produced in the rectangular loop of wire ABCD if its resistance is R, Fig

View SolutionA rectangular loop of wire ABCD is kept close to an infinitely long wire carring a current I (t) =I0(1=t/T) for 0≤t≤ and I (0) for t gt T, Fig. Find the total charges passing through a given point in the loop, in time T. resistance of the loop is R
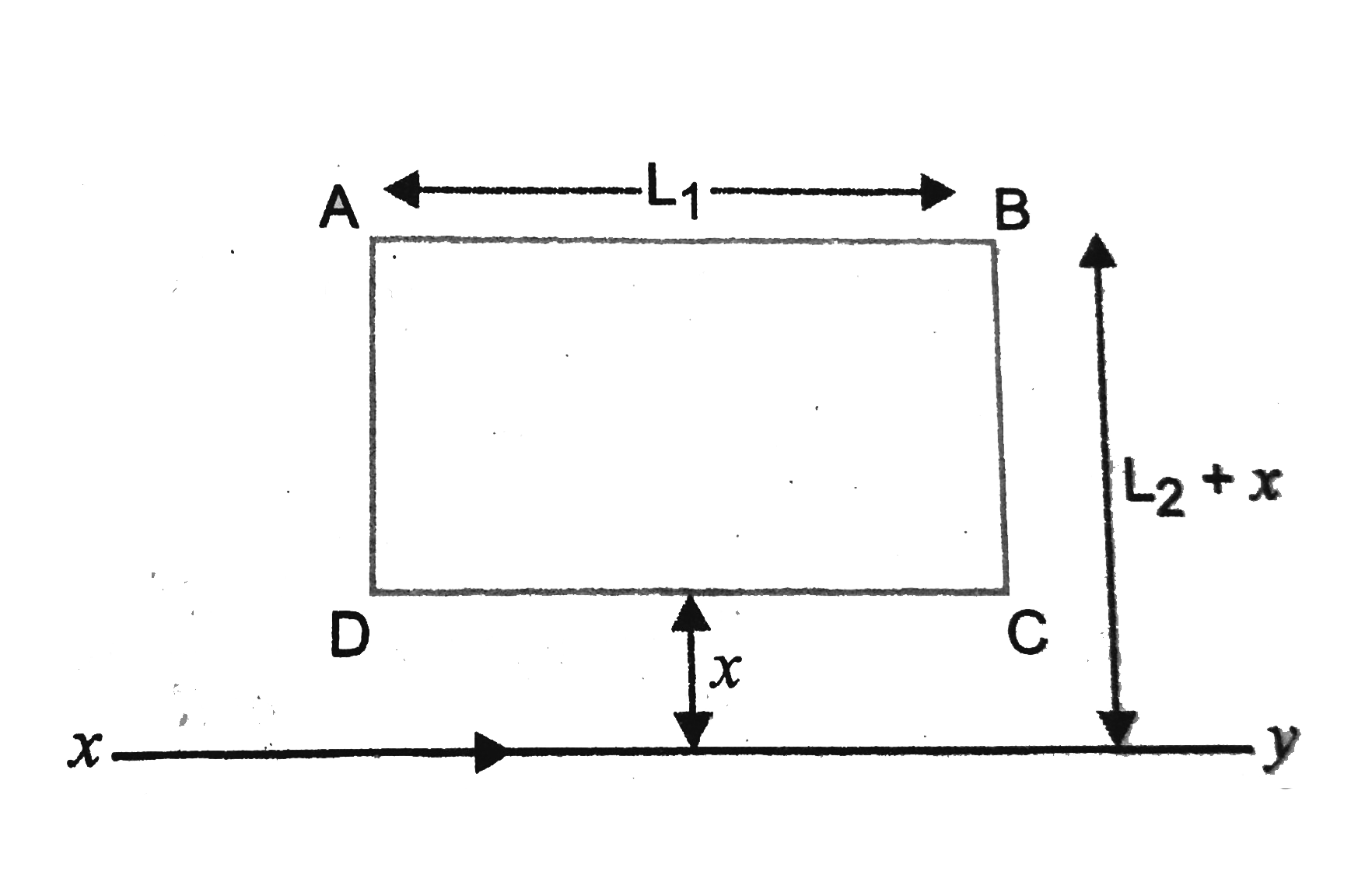
View SolutionA long straight wire is parallel to one edge of a rectangular loop as shown in figure-5.310. if the current in the long wire varies with time as I=I_(0)e^(-tr) , what will be the induced emf in the loop at t= tau ?
View SolutionThe flux of magnetic field through a closed conducting loop of resistance 0.4Ω changes with time according to the equation Φ=0.20t2+0.40t+0.60 where t is time in seconds.Find (i)the induced emf at t=2s.(ii)the average induced emf in t=0 to t=5s.(iii)charge passed through the loop in t=0 to t=5s (iv)average current.In time interval t=0 to t=5s (v) heat produced in t=0 to t=5s
View SolutionIf a current I=4pi sin pi t ampere flows through a wire, then find the amount of charge that flows through the wire in (i) t=0 to t=1s and (ii) t=1 s to t=2s.
View SolutionIn Fig. 30-42, a wire forms a closed circular loop, of radius R = 0.32 m and resistance 0.056 Omega . The circle is centered on a long straight wire, at time t = 0, the current in the long straight wire is 5.0 A rightward. Thereafter, the current changes according to i = 5.0 A - (2.0 A//s^(2))t^(2) . (The straight wire is insulated, so there is no electrical contact between it and the wire of the loop.) What is the magnitude of the current induced in the loop at times t gt 0 ?
View SolutionConsider an infinitely long wire carrying a current I(t), with (dI)/(dt)=lambda = constant. Find the dt current produced in the rectangular loop of wire ABCD if its resistance is R as in figure.
View SolutionConsider an infinitely long wire carrying a current I (t), With (dI)/(dt) = lambda = constant . Find the current produced in the rectangular loop of wire ABCD if its resistance is R, Fig
View Solution

