ODBAC is a fixed rectangular conductor of negligible resistance (CO is not connected) and OP is a conductor which rotates clockwise with an angular velocity $ω$ as figure. The entire system is in a uniform magnetic field B whose direction is along the normal to the surface of the rectangular conductor ABDC. The conductor OP is in electric contact with ABDC. The rotating conductor has a resistance of $λ$ per unit length. Find the current in the rotating conductor, as it rotates by $180^{\circ}$ .
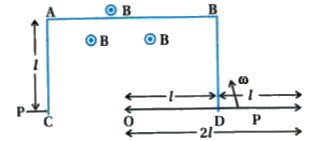Solution in Gujrati

Video Solution

Text Solution

Verified by Experts

(i)Considering situation of OP wire after
$t = \frac{I}{8} = \frac{π}{4 ω}$

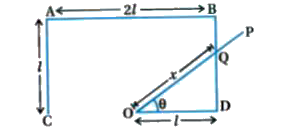
Suppose at this instance wire OP intercept BD at Q. Suppose OQ is x.
Area of $Δ O D Q = \frac{1}{2} \times O D \times Q D$
$= \frac{1}{2} \times l \times < a n θ$
$[∵ tan θ = \frac{Q D}{O D} = \frac{Q D}{l}]$
$= \frac{1}{2} l^{2} tan θ$
Flux linked with $Δ O D Q,$
$ϕ = A B = \frac{1}{2} l^{2} tan θ B = \frac{1}{2} l^{2} B tan (ω t) (∵ θ = ω t)$
Induced emf ,
$ε = \frac{d ϕ}{d t} = \frac{d}{d t} (\frac{1}{2} l^{2} B tan (ω t))$
$= ε = \frac{1}{2} B l^{2} ω^{2} {sec}^{2} ω t$
Induced current,
$I = \frac{ε}{R} = \frac{ε}{λ x}$ (Here only x length of wire OP is inside closed loop , hence resistance $R = λ x$ )
Now $cos θ = \frac{l}{x} \Rightarrow x = \frac{l}{cos θ} = \frac{l}{cos ω t}$
$∴ I = \frac{ε}{λ l} cos ω t = \frac{1}{λ l} . \frac{1}{2} B l^{2} ω {sec}^{2} ω t cos ω t$
$∴ I = \frac{1}{2} \frac{B l ω}{λ cos ω t}$
(ii) For $t = \frac{T}{8} = \frac{π}{4 ω}$ to $t = \frac{3 T}{8} = \frac{3 π}{4 ω}$

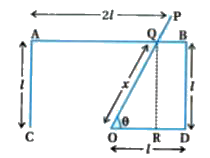
In this case wire OP intercept AB at Q suppose OQ =x
Flux linked with closed loop OQBDO
$ϕ = A B = B (l^{2} + \frac{l^{2}}{2 tan θ})$
$ϕ = B l^{2} (1 + \frac{1}{2} cos ω t) (θ = ω t)$
Induced emf ,
$ε = - \frac{d ϕ}{d t}$
$= - \frac{d}{d t} B l^{2} (1 + \frac{1}{2} cot (ω t))$
$= - B l^{2} \times \frac{1}{2} [- {cosec}^{2} (ω t)] (ω)$
$ε = \frac{1}{2} B l^{2} ω {cosec}^{2} (ω t)$
Induced current $I = \frac{ε}{R} = \frac{ε}{λ x} = \frac{ε sin ω t}{λ l}$
$(sin θ = \frac{l}{x} \Rightarrow x = \frac{l}{sin ω t})$
$I = \frac{1}{λ l} \times \frac{1}{2} B l^{2} ω {cosec}^{2} (ω t) . sin (ω t)$
$I = \frac{1}{2} \frac{B l ω}{λ sin (ω t)}$
(iii) Now $t = \frac{3 T}{8} = \frac{3 ω}{4 π}$ to $t = \frac{T}{2} = \frac{π}{ω}$
Suppose wire PQ intercept AC at Q and OQ =x (see figure)

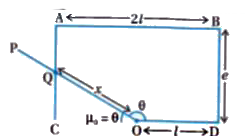
Flux linked with closed loop OQABDO is ,
$ϕ = B A = B (2 l^{2} - \frac{l^{2}}{2 tan (ω t)})$
Induced emf,
$ε = \frac{d ϕ}{d t}$
$= \frac{d}{d t} [B l^{2} (2 - \frac{1}{2 tan (ω t)})]$
$= \frac{B l^{2}}{2} ω {cosec}^{2} (ω t)$
Induced current ,
$I = \frac{ε}{R} = \frac{ε}{λ x} = \frac{ε}{λ l} sin (ω t)$
$= \frac{1}{λ l} sin (ω t) . \frac{B l^{2} ω}{2} {cos}^{2} (ω t)$
$= \frac{1}{2} \frac{B l ω}{λ sin (ω t)}$

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

Topper's Solved these Questions

Similar Questions

KUMAR PRAKASHAN-ELECTROMAGNETIC INDUCTION-Section C Ncert Exemplar Solution (Long Answer )

Home
Ask Doubt
Profile