The greater and least resultant of two forces are 7 N and 3 N respectively. If each of the force is increased by 3N and applied at 60°. The magnitude of the resultant isSolution in Telugu
7 N
3 N
10 N
√129N
The correct Answer is:D
Step by step video, text & image solution for The greater and least resultant of two forces are 7 N and 3 N respectively. If each of the force is increased by 3N and applied at 60°. The magnitude of the resultant is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MOTION IN A PLANEBook:AAKASH SERIESChapter:MOTION IN A PLANEExercise:EXERCISE-2 (Lami.s theorem :)
Explore 8 Videos
- MOTION IN A PLANEBook:AAKASH SERIESChapter:MOTION IN A PLANEExercise:EXERCISE-2 ( Relative velocity)
Explore 15 Videos
- MOTION IN A PLANEBook:AAKASH SERIESChapter:MOTION IN A PLANEExercise:EXERCISE-IB (Circular motion)
Explore 12 Videos
- MAGNETISMBook:AAKASH SERIESChapter:MAGNETISMExercise:PROBLEMS (LEVEL-II)
Explore 13 Videos
- MOTION IN A PLANEBook:AAKASH SERIESChapter:MOTION IN A PLANEExercise:QUESTION FOR DESCRIPTIVE ANSWER
Explore 7 Videos
Similar Questions
If 'O' is at equilibrium then the values of the tension T1andT2 are x, y, if 20 N is vertically down. Then x, y are
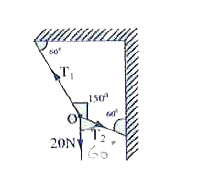
View SolutionA train of 150 metre length is going towards north direction at a speed of 10 m/s. A parrot flies at the speed of 5 m/s towards south direction parallel to the railways track. The time taken by the parrot to cross the train is
View Solution(A): When a particle moves in a circle with a uniform speed, its velocity and accele ration both changes.
(R): The centripetal acceleration in circular motion is dependent on angular velocity of the body.
View SolutionThe force between the two poles is reduced to 'x' newtons when their separation is increased n times. It is increased by 'y' newtons when their separation is made 1/nth of their original value. What is the relation between x and y?
View SolutionA particle is projected over a triangle from one end of a horizontal base and garzing the vertex falls on the other end of the base . If α and β the base angles and θ the angle of projection then show that tanθ=tanα+tanβ.
View SolutionThe greatest and least resultant of two forces are 7N and 3N respectively. If each of the force is increased by 3N and applied at 60∘.The magnitude of the resultant is
View SolutionTwo forces of magnitudes 3N and 4 N act together on an object making an angle 60^(@) with each other. Find the resultant force acting on the object.
View SolutionTwo forces are such that the sum of their magnitudes is 18N and their resultant is 12 N which is perpendicular to the smaller force. Then the magnitude of the forces are
View SolutionThe greatest and least resultant of two forces acting at a point are 29N and 5N. If each force is increased by 3N, find the magnitude of the resultant of the two new forces when they act at right angles to each other.
View SolutionTwo forces A and B are acting at a point . The least and greatest resultants of these forces are 5 N and 10 N respectively . If each of these forces is decreased by 2 N , then what will be the resultant of these new forces acting at an angle of 30∘ to each other ?
View SolutionThe greater and least resultant of two forces are 7 N and 3 N respectively. If each of the force is increased by 3N and applied at 60°. The magnitude of the resultant is
View SolutionThe greater and least resultant of two forces are 9 N and 5 N respectively. If they are applied at 60°. The magnitude of the resultant is
View SolutionThe resultant of two whose magnitudes are in the ratio 3:5 is 28 N . If the angle of their inclination is 60∘ then find the magnitude of each force .
View SolutionThe greater and least resultant of two forces are 7 N and 3 N respectively. If each of the force is increased by 3N and applied at 60^(@) . The magnitude of the resultant is
View SolutionThe greater and least resultant of two forces are 7 N and 3 N respectively. If each of the force is increased by 3N and applied at 60∘. The magnitude of the resultant is
View Solution

