Two forces of magnitudes 3N and 4 N act together on an object making an angle 60∘ with each other. Find the resultant force acting on the object.
To find the resultant force acting on an object when two forces of magnitudes 3 N and 4 N act at an angle of 60 degrees to each other, we can use the formula for the resultant of two vectors:
1. Identify the Forces and the Angle:
- Let F1=3N (first force)
- Let F2=4N (second force)
- The angle between the two forces, θ=60∘.
2. Use the Formula for Resultant Force:
The formula for the resultant R of two forces F1 and F2 at an angle θ is given by:
R=√F21+F22+2F1F2cosθ
3. Substitute the Values:
- Calculate F21:
F21=32=9
- Calculate F22:
F22=42=16
- Calculate 2F1F2cosθ:
- First, find cos60∘:
cos60∘=12
- Now substitute into the equation:
2F1F2cosθ=2×3×4×12=12
4. Combine the Values:
Now plug these values into the resultant formula:
R=√9+16+12
R=√37
5. Calculate the Resultant:
The resultant force is:
R≈6.08N(since √37≈6.08)
Final Answer:
The resultant force acting on the object is approximately 6.08N.
---
- Let F1=3N (first force)
- Let F2=4N (second force)
- The angle between the two forces, θ=60∘.
The formula for the resultant R of two forces F1 and F2 at an angle θ is given by:
R=√F21+F22+2F1F2cosθ
- Calculate F21:
F21=32=9
- Calculate F22:
F22=42=16
- Calculate 2F1F2cosθ:
- First, find cos60∘:
cos60∘=12
- Now substitute into the equation:
2F1F2cosθ=2×3×4×12=12
Now plug these values into the resultant formula:
R=√9+16+12
R=√37
The resultant force is:
R≈6.08N(since √37≈6.08)
The resultant force acting on the object is approximately 6.08N.
Topper's Solved these Questions
- MOTION IN A PLANEBook:AAKASH INSTITUTEChapter:MOTION IN A PLANEExercise:llustration 1 :
Explore 1 Video
- MOTION IN A PLANEBook:AAKASH INSTITUTEChapter:MOTION IN A PLANEExercise:Try yourself
Explore 48 Videos
- MOCK_TEST_17Book:AAKASH INSTITUTEChapter:MOCK_TEST_17Exercise:Example
Explore 15 Videos
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN A STRAIGHT LINEExercise:ASSIGNMENT (SECTION - D)
Explore 15 Videos
Similar Questions
Knowledge Check
Two equal forces acting at 60∘ to each other. Find the forces if resultant force is 300 N.
A155.3NB173.2 NC162.4 NDNone of theseTwo equal forces acting at 60∘ to each other. Find the forces if resultant force is 300 N.
A155.3 NB173.2 NC162.4 NDNone of theseA body is acted upon by two forces of manitudes F1=√2NandF2=3N which are inclined at 45∘ to each other. There magnitude of resultant force acting on the body is
A17 NB11 NC√17ND√11N
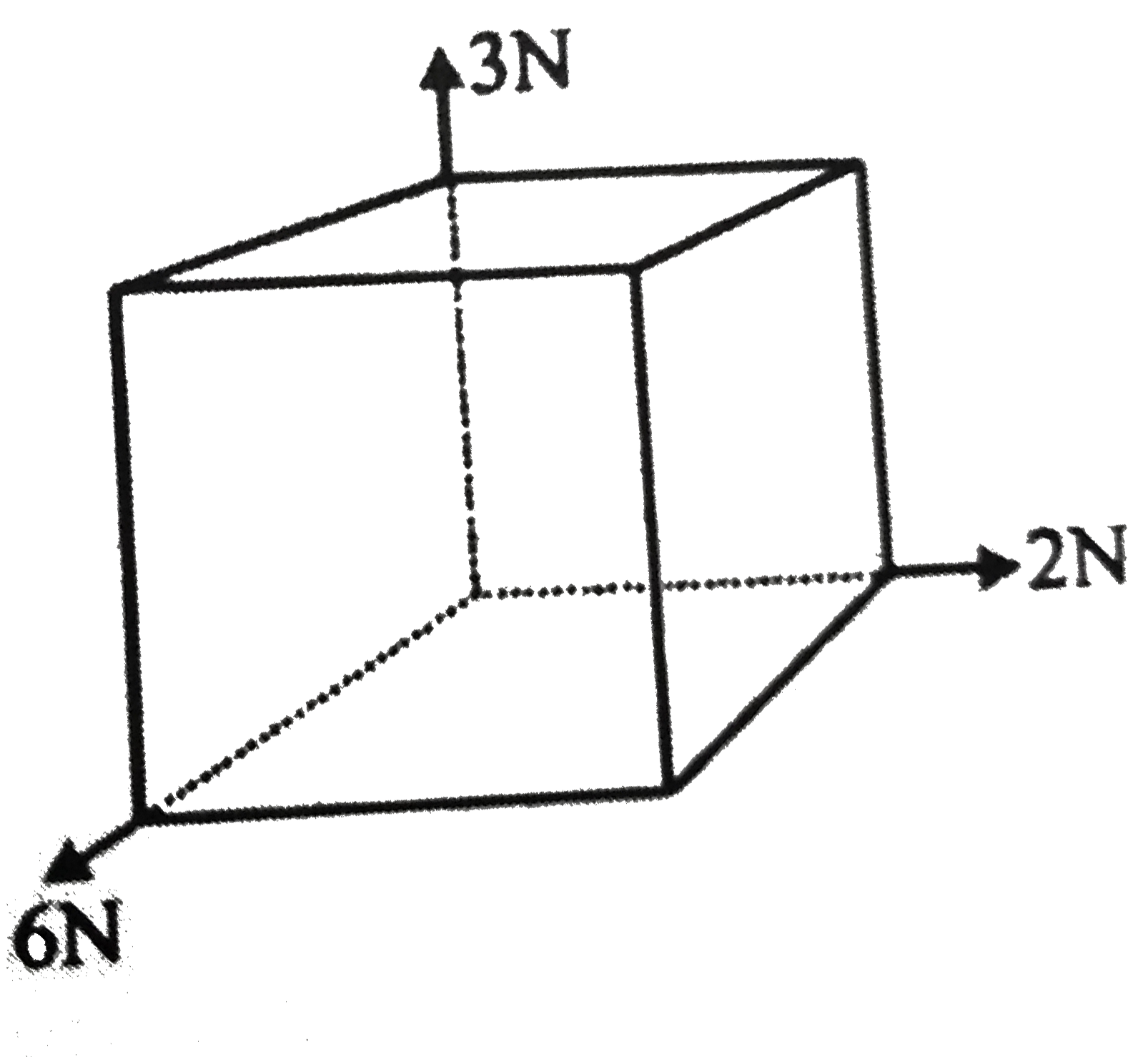
Three forces of magnitudes 2N, 3N and 6N act at corners of a cube along three sides as shown in figure. Find the resultant of these forces in N.
View SolutionTwo forces of equal magnitude act at a point making an angle θ with each other. If the direction of one of the forces is reversed, the direction of the resultant will turn through
View SolutionA body of mass 10 kg is acted upon by two forces each of magnitude 10 N making an angle of 60∘ with each other. Find the net acceleration of the body
View SolutionTwo forces of magnitudes 3N and 4N are acted on a body. The ratio of magnitude of minimum and maximum resultant force on the body is
View SolutionTwo forces each of magnitude 2N, act at an angle of 60∘. What is the magnitude of the resultant force ?
View Solution

