Two forces of magnitudes 3N and 4 N act together on an object making an angle 60∘ with each other. Find the resultant force acting on the object.
To find the resultant force acting on an object when two forces of magnitudes 3 N and 4 N act at an angle of 60 degrees to each other, we can use the law of cosines. Here’s the step-by-step solution:
Step 1: Identify the Forces and the Angle
Let:
- A=3N (magnitude of the first force)
- B=4N (magnitude of the second force)
- θ=60∘ (angle between the two forces)
Step 2: Use the Formula for Resultant Force
The magnitude of the resultant force C can be calculated using the formula:
C=√A2+B2+2ABcos(θ)
Step 3: Substitute the Values into the Formula
Substituting the values of A, B, and θ:
C=√32+42+2⋅3⋅4⋅cos(60∘)
Step 4: Calculate Each Component
1. Calculate A2:
32=9
2. Calculate B2:
42=16
3. Calculate cos(60∘):
cos(60∘)=12
4. Calculate 2ABcos(60∘):
2⋅3⋅4⋅12=12
Step 5: Combine the Results
Now substitute these values back into the equation:
C=√9+16+12
C=√37
Step 6: Final Result
The magnitude of the resultant force C is:
C≈6.08N
Let:
- A=3N (magnitude of the first force)
- B=4N (magnitude of the second force)
- θ=60∘ (angle between the two forces)
The magnitude of the resultant force C can be calculated using the formula:
C=√A2+B2+2ABcos(θ)
Substituting the values of A, B, and θ:
C=√32+42+2⋅3⋅4⋅cos(60∘)
1. Calculate A2:
32=9
2. Calculate B2:
42=16
3. Calculate cos(60∘):
cos(60∘)=12
4. Calculate 2ABcos(60∘):
2⋅3⋅4⋅12=12
Now substitute these values back into the equation:
C=√9+16+12
C=√37
The magnitude of the resultant force C is:
C≈6.08N
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - llustration 1 :
1 Video
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Try yourself
48 Videos
- MOCK_TEST_17BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOCK_TEST_17EXERCISE - Example
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
Similar Questions
Two forces of magnitudes 3N and 4N are acted on a body. The ratio of magnitude of minimum and maximum resultant force on the body is
View SolutionThree forces of magnitudes 2N, 3N and 6N act at corners of a cube along three sides as shown in figure. Find the resultant of these forces in N.
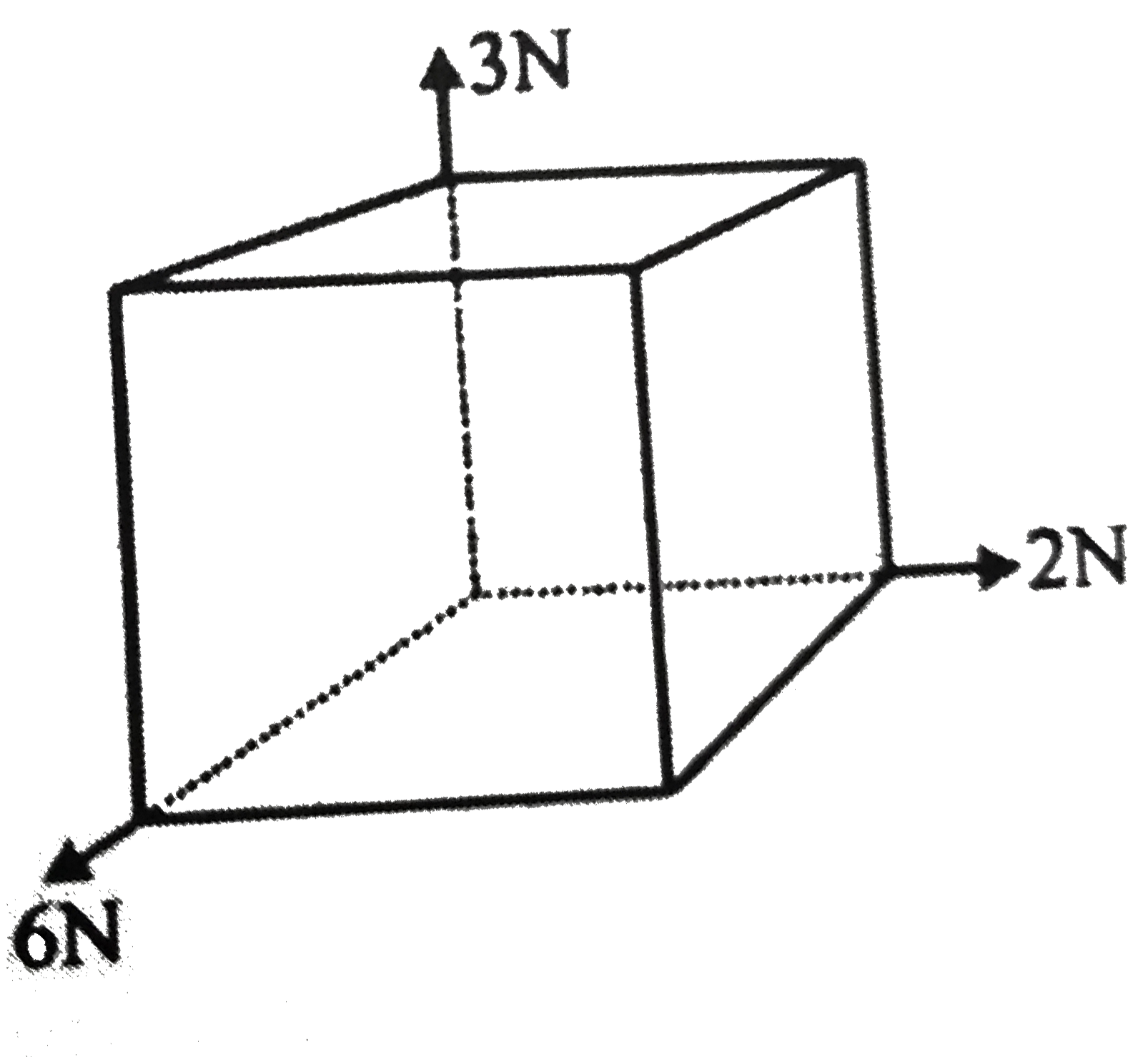
View Solution
Knowledge Check
Two forces each of magnitude 2N, act at an angle of 60∘. The magnitude of the resultant force
A√1.1 NewtonB√4 NewtonC√12 NewtonD√14.9 NewtonA body of mass 2kg is acted by two forces each of magnitude 1 newton, making an angle of 60∘ with each other. The net acceleration of the body (inm/s2) is
A0.5B1C√3/2D√2/3
Two forces of unequal magnitude simultaneously act on a particle making an angle θ(=120∘) with each other.If one of them is reversed ,the accelaration of the particle is become √3 times. Calculate the ratio of the magnitude of the forces.
View SolutionA block is applied two forces of magnitude 5N each. One force is acting towards East and the other acting along 60∘ North of East. The resultant of the two forces (in N) is of magnitude :-
View SolutionTwo forces of magnitudes 3N and 4N respectively are acting on a body. Calculate the resultant force if the angle between them is- 90
View SolutionTwo forces of magnitude 3N and 4N respectively are acting on a body. Calculate the resultant force if the angle between them is
0∘
View SolutionTwo forces of magnitudes 3N and 4N respectively are acting on a body. Calculate the resultant force if the angle between them is-
180∘
View SolutionA body, acted upon by a force of 50N, is displaced through a distance 10m in direction making an angle of 60∘ with the force. Find the work done by the force.
View Solution
