A piece of uniform string hangs vertically so that its free end just touches horizontal surface of a table. The upper end of the string is now released. Show that at any instant during the falling of string, the total force on the surface is three times the weight of that part of string lying on the surface.Solution in Telugu
Let m be the mass per unit length of string and x the length of string at any instant on the table. If differential length dx of string further falls in time dt, then velocity v of this element will be given by
v2=u2+2gx
orv2=0+2gx ........ (1)
orv2=gx ......... (2)
Net force on the surface of the table
F=dpdt+ weight of string lying on the surface
=mdx.vdt+mxg=mvdxdt+mxg=mv2+mgx
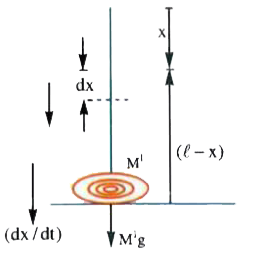
Using (1) , F=m(2gx)+mgx=3(mx)g
Butmx=M1= weight of string lying on the table
∴F=3M1g
Topper's Solved these Questions
- LAWS OF MOTIONBook:AAKASH SERIESChapter:LAWS OF MOTIONExercise:LONG ANSWER TYPE QUESTIONS
Explore 4 Videos
- LAWS OF MOTIONBook:AAKASH SERIESChapter:LAWS OF MOTIONExercise:SHORT ANSWER TYPE QUESTION
Explore 5 Videos
- GEOMETRICAL OPTICSBook:AAKASH SERIESChapter:GEOMETRICAL OPTICSExercise:ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
Explore 6 Videos
- LOGIC GATESBook:AAKASH SERIESChapter:LOGIC GATESExercise:Exercise (Very Short Answer)
Explore 16 Videos
Similar Questions
State Newton's three laws of motion and derive the relation F= ma.
View SolutionState the Newton's laws of motion. What is the SI unit of force ?
View SolutionA fish is at a depth of 12 cm in water is viewed by an observer on the bank of a lake. To what height the image of the fish is raised in cm ?
View SolutionName the output function in the following circuit

View SolutionA string secured at its ends is stretched with a force of tension F. The mass of the string and the force of gravity can be neglected. A point weight with a mass m is attached to the middle of the string. The time period of small oscillations of the weight is 2π√mlxF. the value of x is ________
(Neglect any change in the magnitude of tension of the string during oscillations)

View SolutionA uniform thick string of length 5 m is resting on a horizontal frictionless surface. It is pulled by a horizontal force of 5 N from one end. The tension in the string at 1m from the force applied is :
View SolutionA string wrapped around a cyliner of mass m and radius R . The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder. Acceleration of hanging mass is:
View SolutionA string wrapped around a cyliner of mass m and radius R . The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder. Acceleration of cylinder is:
View SolutionA string wrapped around a cyliner of mass m and radius R . The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder. Velocity of point of contact 'of cylinder at this moment is:
View SolutionA string wrapped around a cyliner of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
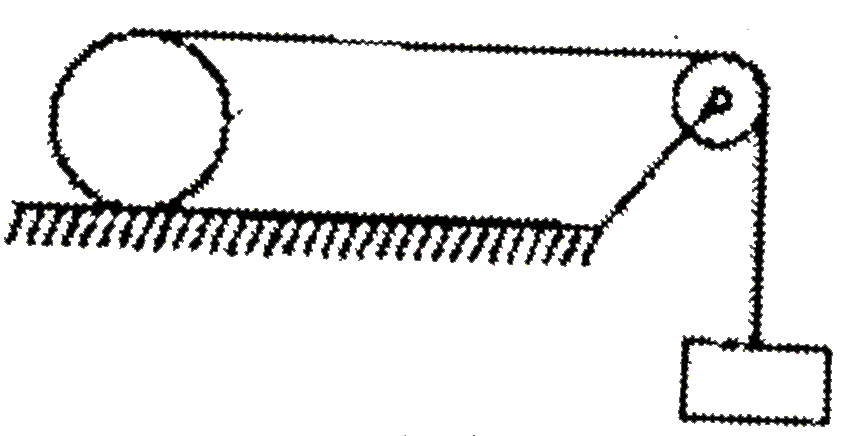
Velocity of hanging block at this moment is: is:
View SolutionA string of length L and mass M is lying on a horizontal table. A force F is applied at one of its ends. Tension in the string at a distance x from the end at which force is applied is
View SolutionA perfectly elastic uniform string is suspended vertically with its upper end fixed to the ceiling and the lower end loaded with the weight. If a transverse wave is imparted to the lower end of the string, the pulse will
View SolutionA piece of uniform string hangs vertically so that its free end just touches horizontal surface of a table. The upper end of the string is now released. Show that at any instant during the falling of string, the total force on the surface is three times the weight of that part of string lying on the surface.
View SolutionA string of length L and mass M is lying on a horizontal table. A force F is applied at one of its ends. Tension in the string at a distance x from the end at which force is applied is
View SolutionA piece of uniform string hangs vertically so that its free end just touches horizontal surface of a table . The upper end of the string is now released . Show that at any instant during the falling of string , the total force on the surface is three times the weight of that part of string lying on the surface .
View Solution

