A uniform thick string of length 5 m is resting on a horizontal frictionless surface. It is pulled by a horizontal force of 5 N from one end. The tension in the string at 1m from the force applied is :
zero
5N
4N
1N
The correct Answer is:3
To solve the problem, we need to determine the tension in the string at a point 1 meter from the end where a 5 N force is applied. We can follow these steps:
1. Identify the System:
We have a uniform thick string of length 5 m resting on a frictionless surface. A force of 5 N is applied horizontally at one end.
2. Define Mass of the String:
Let the total mass of the string be m. Since the string is uniform, the mass per unit length is m5 kg/m.
3. Calculate Acceleration:
The net force acting on the entire string is equal to the applied force. According to Newton's second law, we have:
Fnet=m⋅a
Here, Fnet=5N. Therefore,
5=m⋅a⟹a=5m
4. Consider the Segment of the String:
We will analyze the segment of the string that is 1 m long, which is the part of the string at a distance of 1 m from the point where the force is applied. The mass of this 1 m segment is:
msegment=m5kg
5. Apply Newton's Second Law to the Segment:
For the 1 m segment, the forces acting on it are the tension T at the end of the segment and the applied force of 5 N. According to Newton's second law:
5−T=msegment⋅a
Substituting the values we have:
5−T=(m5)⋅(5m)
6. Simplify the Equation:
The right side simplifies to:
5−T=1
Therefore, we can solve for T:
T=5−1=4N
7. Conclusion:
The tension in the string at 1 m from the force applied is T=4N.
Final Answer:
The tension in the string at 1 m from the force applied is 4 N.
We have a uniform thick string of length 5 m resting on a frictionless surface. A force of 5 N is applied horizontally at one end.
Let the total mass of the string be m. Since the string is uniform, the mass per unit length is m5 kg/m.
The net force acting on the entire string is equal to the applied force. According to Newton's second law, we have:
Fnet=m⋅a
Here, Fnet=5N. Therefore,
5=m⋅a⟹a=5m
We will analyze the segment of the string that is 1 m long, which is the part of the string at a distance of 1 m from the point where the force is applied. The mass of this 1 m segment is:
msegment=m5kg
For the 1 m segment, the forces acting on it are the tension T at the end of the segment and the applied force of 5 N. According to Newton's second law:
5−T=msegment⋅a
Substituting the values we have:
5−T=(m5)⋅(5m)
The right side simplifies to:
5−T=1
Therefore, we can solve for T:
T=5−1=4N
The tension in the string at 1 m from the force applied is T=4N.
The tension in the string at 1 m from the force applied is 4 N.
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
A uniform rope of length 10m is on a smooth horizontal surface. It is being pulled by a horizontal force of 20N at one end. The ratio of tension at a distance of 4m from force end to tension at a distance of 4m from free end is
View Solution[" A uniform rope of length "5m" is "],[" on a smooth horizontal "],[" surface.It is being pulled by a "],[" horizontal force of "20N" at one "],[" end.The ratio of tension at a "],[" distance of "2m" from force end "],[" to tension at a distance of "2m],[" from free end is "]
View Solution
Knowledge Check
A string of length L and mass M is lying on a horizontal table. A force F is applied at one of its ends. Tension in the string at a distance x from the end at which force is applied is
AZeroBFCF(L−y)LDF(l−y)MA string of length L and mass M is lying on a horizontal table. A force F is applied at one of its ends. Tension in the string at a distance x from the end at which force is applied is
AZeroBF should be equal to the weight of A and BCF(L-x)/LDF(L-x)MA rope of length 4 m having mass 1.5 kg/m lying on a horizontal frictionless surface is pulled at one end by a force of 12N. What is the tension in the rope at a point 1.6 m from the other end?
A5NB4.8NC7.2ND6N
A uniform rope of length L , resting on frictionless horizontal table is pulled at one end by a force F . What is the tension in the rope at a distance x from the end where the force is applied ?
[ Hint : Consider the motion of the entire rope and the motion of x length of rope using P = ma formula and third law of motion ]
View SolutionA rope of length 5 m is kept on frictionless surface and a force of 5 N is applied to one of its end. Find the tension in the rope at 1 m from this end
View SolutionA rope of length 20 cm is kept on frictionless surface and a force of 5 N is applied to one of its end. Find the tension in the rope at 5m from this end.
View SolutionAn object rests on a horizontal frictionless surface. A horizontal force of magnitude F is applied. This force produces an acceleration
View SolutionThree masses are connected as shown in figure on a horizontal frictionless surface and pulled by a force of 60 N. The tensions T1andT2 are in the ratio
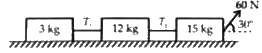
View Solution