Boxes A and B are sliding to the right across a frictionless table. The hand H is slowing them down. The mass of A is larger than the mass of B. rank in order, from largest to samllest, the horizontal forces on A,B and H.
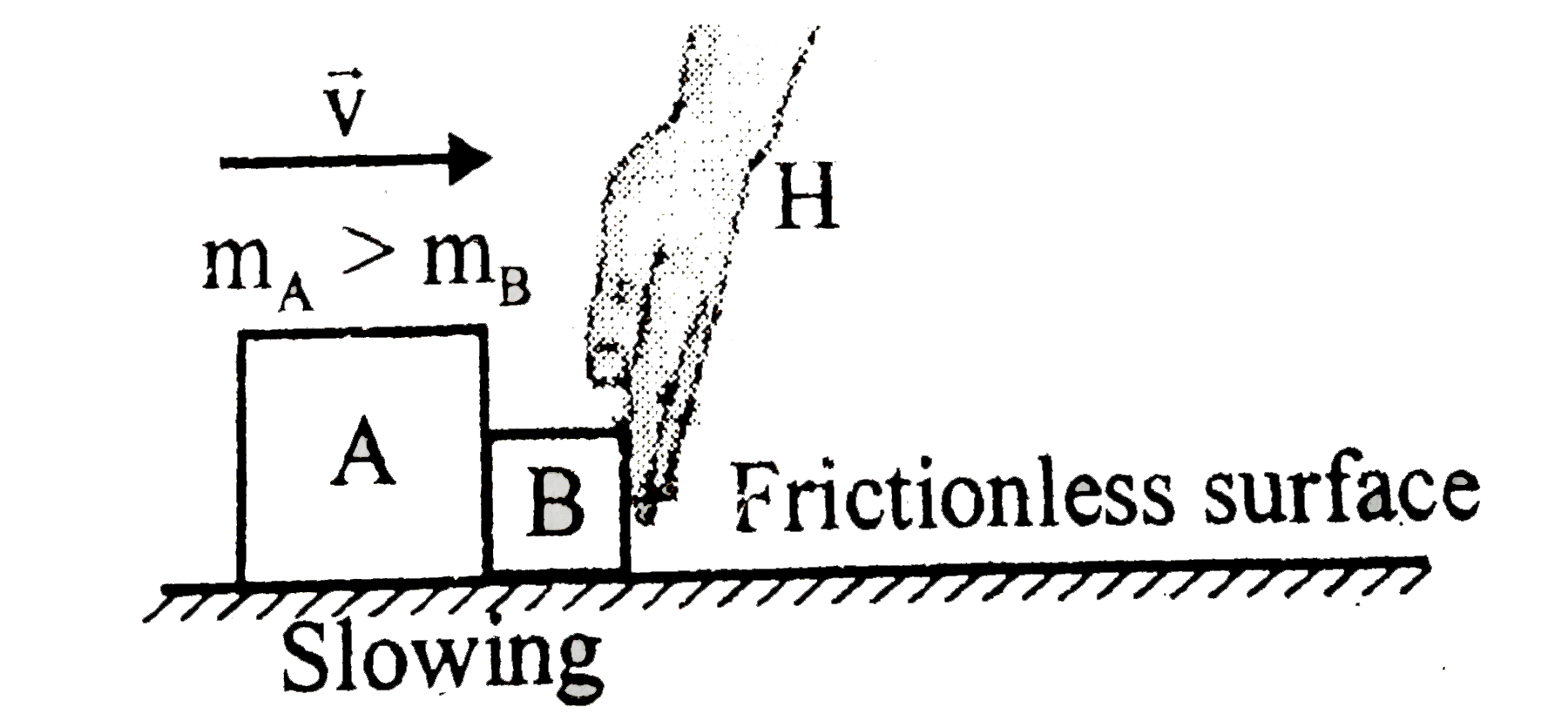
FB on H=FH on B=FA on B=F B on A
FB on H=FH on B>FA on B=F B on A
FB on H=FH on B<FA on B=F B on A
FB on H=FH on B>FA on B>F B on A
The correct Answer is:2
FBonH=FHonB and FAonB=FBonA because therse are action / reaction pairs. Box B is slowing down and therefore must have a net force to the left. So from Newton's second law we also know that FHonB>FAonB
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
Three metal blocks A , B and C of masses 10 kg , 20 kg and 30 kg rest on a frictionless table in a line . A is converted to B and B to C by two pieces of string . With the help of a third string attached to C , the system is pulled to the right with a force of 60 N . Find the tensions of the first and second strings .
View SolutionTwo blocks A and B of masses mA and mB are connected together by means of a spring and are resting on a horizontal frictionless table. The blocks are then pulled apart so as to stretch the spring and then released. Show that the kinetic energies of the blocks are, at any instant inversely proportional to their masses.
View Solution
Knowledge Check
Two blocks of masses m and M are placed on a horizontal frictionless table connected by light spring as shown in the figure. Mass M is pulled to the right with a force F. If the acceleration of mass m is a, then the acceleration of mass M will be
 A(F−ma)MB(F+ma)MCFMDamM
A(F−ma)MB(F+ma)MCFMDamMTwo blocks of masses m and M are placed on a horizontal frictionless table connected by light spring as shown in figure. The Mass M is pulled to the right with a force F It the acceleration of mass m is a then the acceleration of M will be .
 A(F−ma)MB(F+ma)MCFMDamM
A(F−ma)MB(F+ma)MCFMDamMA block of mass m starts at rest at height on a frictionless inclined plane. The block slides down the plane, travels across a rough horizontal surface with coefficient of kinetic friction μ and compresses a spring with force constant k a distance x before momentarilly coming to rest. Then the spring extends and the block travels back across the rough surface, sliding up the plane. The block travels a total distance d on rough horizontal surface. The correct experssion for the maximum height h' that the block reaches on its return is :
 Amgh'=mgh−μmgdBmgh'=mgh+μmgdCmgh'=mgh+μmgd+kx2Dmgh'=mgh−μmgd−kx2
Amgh'=mgh−μmgdBmgh'=mgh+μmgdCmgh'=mgh+μmgd+kx2Dmgh'=mgh−μmgd−kx2
A chain of mass m and length l lies on a horizontal table. The chain is allowed to slide down gently from the side of the table. Find the speed of the chain at the instant when last link of the chain slides from the table. Neglect friction everywhere.
(a) the force from thelicopter and
(b) the gravitational force on her
(c ) What are speed ot the kinetic energy and.
(d) the speed of the astronaut just before she reaches the helicopter?
View SolutionA block of mass m slides along a frictionless surfce as shown in the figure. If it is releases from rest t A what is its speed at B?

View SolutionA uniform frictionless ring of mass M and radius R, stands vertically on the ground. A wall touches the ring on the left and another wall of height R touches the ring on right (see figure).There is a small bead of mass m positioned at the top of the ring. The bead is given a gentle push and it being to slide down the ring as shown. All surfaces are frictionless.
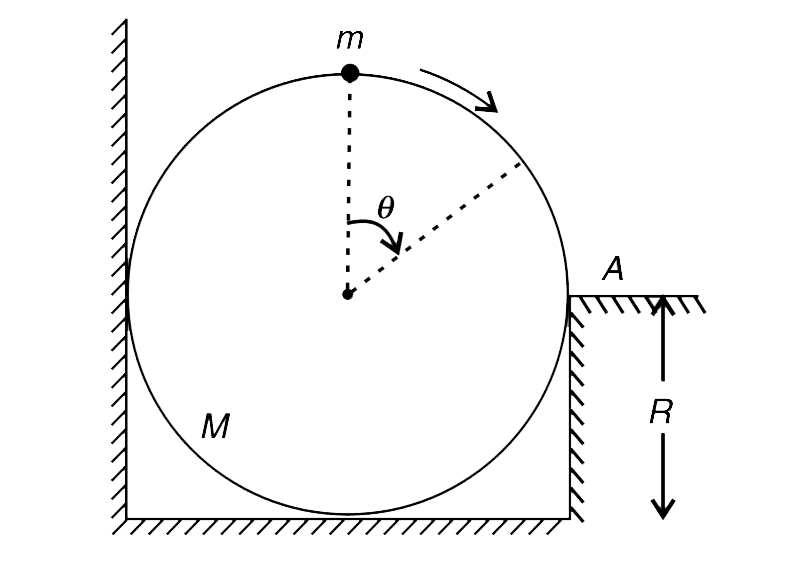
(a) As the bead slides, up to what value of angle θ the force applied by the ground on the ring is larger than Mg?
(b) Write the torque of force applied by the bead on the ring about point A as function of θ.
(c) What is the maximum possible value of torque calculated in (b)? Using this result tell what is the largest value of mM for which the ring never rises off the ground ?
View SolutionTwo blocks of masses 2 kg and 4 kg are in close contact on a frictionless horizontal table. A horizontal force of 18 N is applied to the larger mass. What is the force at the surface of contact between the blocks?
View SolutionThe blocks A and B are arranged as shown in the figure. The pulley is frictionless. The mass of A is 10 kg . The coefficient of friction of A with the horizontal surface is 0.20. The minimum mass of B to start the motion will be
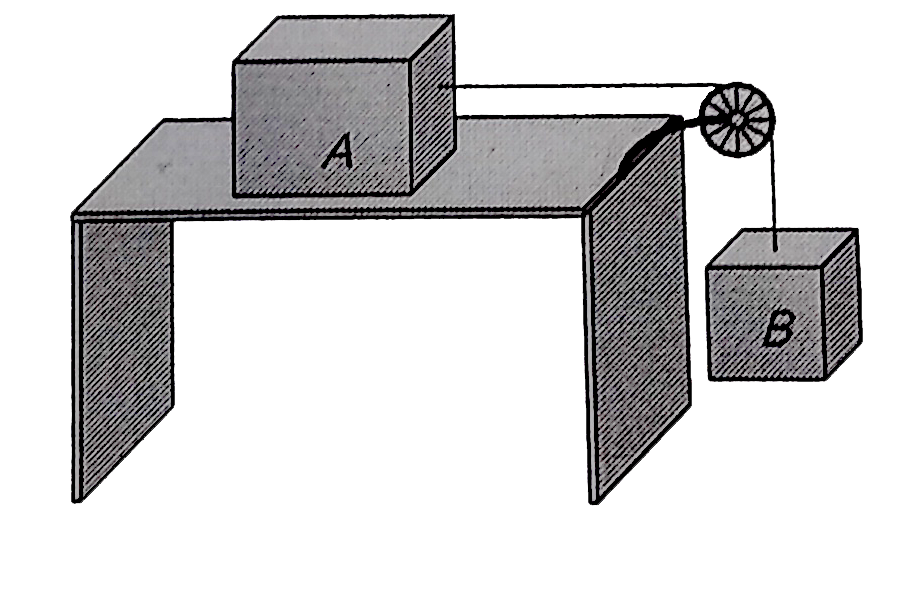
View Solution
