In ΔPQR, D is the mid-point of ¯¯¯¯¯¯QR.then¯¯¯¯¯¯¯PM is ___________,PD is___________. Is QM=MR?
we haveQD=DR
Median of a triangle is a line segment joining a vertex to the midpoint of the opposing side .
∴
PD is median.
¯¯PM
is altitude and perpendicular to QR.
QM≠MR
because D is the mid-point of QR.
Topper's Solved these Questions
- BOOK - NCERT ENGLISHCHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - EXERCISE 6.22videos
THE TRIANGLE AND ITS PROPERTIES
- BOOK - NCERT ENGLISHCHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - EXERCISE 6.58videos
THE TRIANGLE AND ITS PROPERTIES
- BOOK - NCERT ENGLISHCHAPTER - SYMMETRYEXERCISE - EXERCISE 14.22videos
SYMMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One

What is the length of ¯¯¯¯¯¯QR ?A5B5√22C10√2D5√2 - Question 2 - Select One
Given right triangle ΔPQR below, what is the length of ¯¯¯¯¯¯PQ?
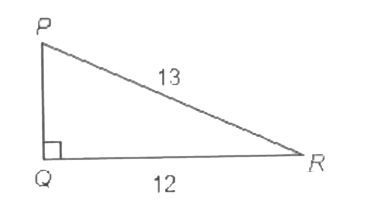 A√2B√5C5D7
A√2B√5C5D7 - Question 3 - Select One
The points P,Q,R and S lie in that order on a straight line . The midpoint of ¯¯¯¯¯¯QS is R and the midpoint of ¯¯¯¯¯PS is Q . The length of ¯¯¯¯¯¯QR is x feet and the length of ¯¯¯¯¯¯PQ is 4x−16 feet . What is the length , in feet , of ¯¯¯¯¯PS?
A32B20C16D8
In ΔPQR, MN is parallel to QR and PMMQ=23
(i) Find MNQR
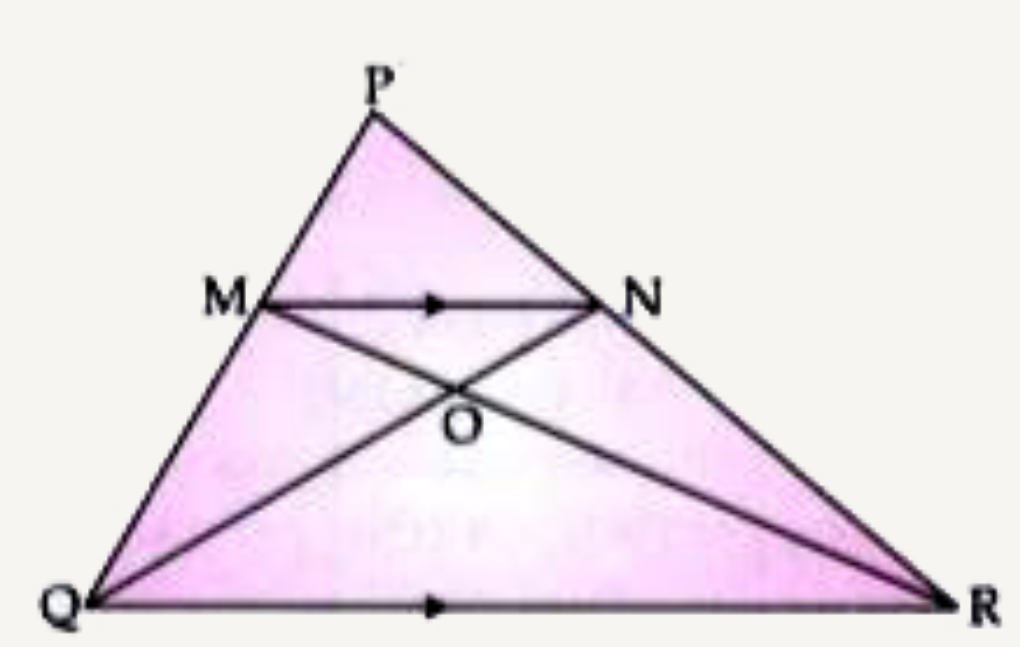 View Solution
View SolutionIn ΔPQR,Pq=PR and S is the mid-point of PQ. A line drawn from S parallel to QR, intersects the line PR at T. Prove that PS = PT.
View SolutionA, B, C, and D all lie on a number line. C is the midpoint of ¯¯¯¯¯¯AB and D is the midpoint of ¯¯¯¯¯¯AC.
Quantity AQuantity BThe ratio of ¯¯¯¯¯¯AD to ¯¯¯¯¯¯CBThe ratio of ¯¯¯¯¯¯AC to ¯¯¯¯¯¯ABView SolutionIn the figure below, ABCD is a rectangle, EFGH is a square, and ¯¯¯¯¯¯CD is a diameter of a semicircle. Point K is the midpoint of ¯¯¯¯¯¯CD. Point J is the midpoint of both ¯¯¯¯¯¯AB and ¯¯¯¯¯¯EF. Points E and F lie on ¯¯¯¯¯¯AB. The 3 given lengths are in meters.
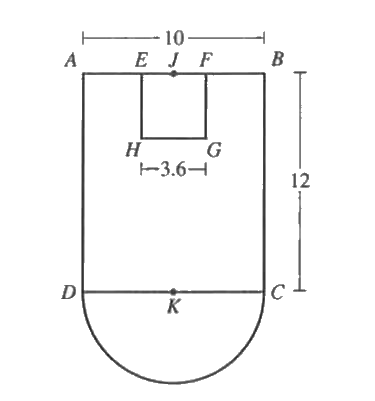
What is the length, in meters, of are ¯¯¯¯¯¯CD?View SolutionIn the figure below, ABCD is a rectangle, EFGH is a square, and ¯¯¯¯¯¯CD is a diameter of a semicircle. Point K is the midpoint of ¯¯¯¯¯¯CD. Point J is the midpoint of both ¯¯¯¯¯¯AB and ¯¯¯¯¯¯EF. Points E and F lie on ¯¯¯¯¯¯AB. The 3 given lengths are in meters.
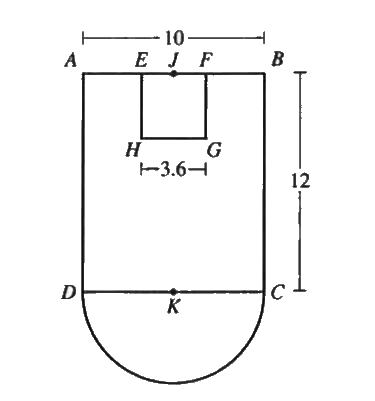
What is the length, in meters, of ¯¯¯¯¯¯JD?View Solution
