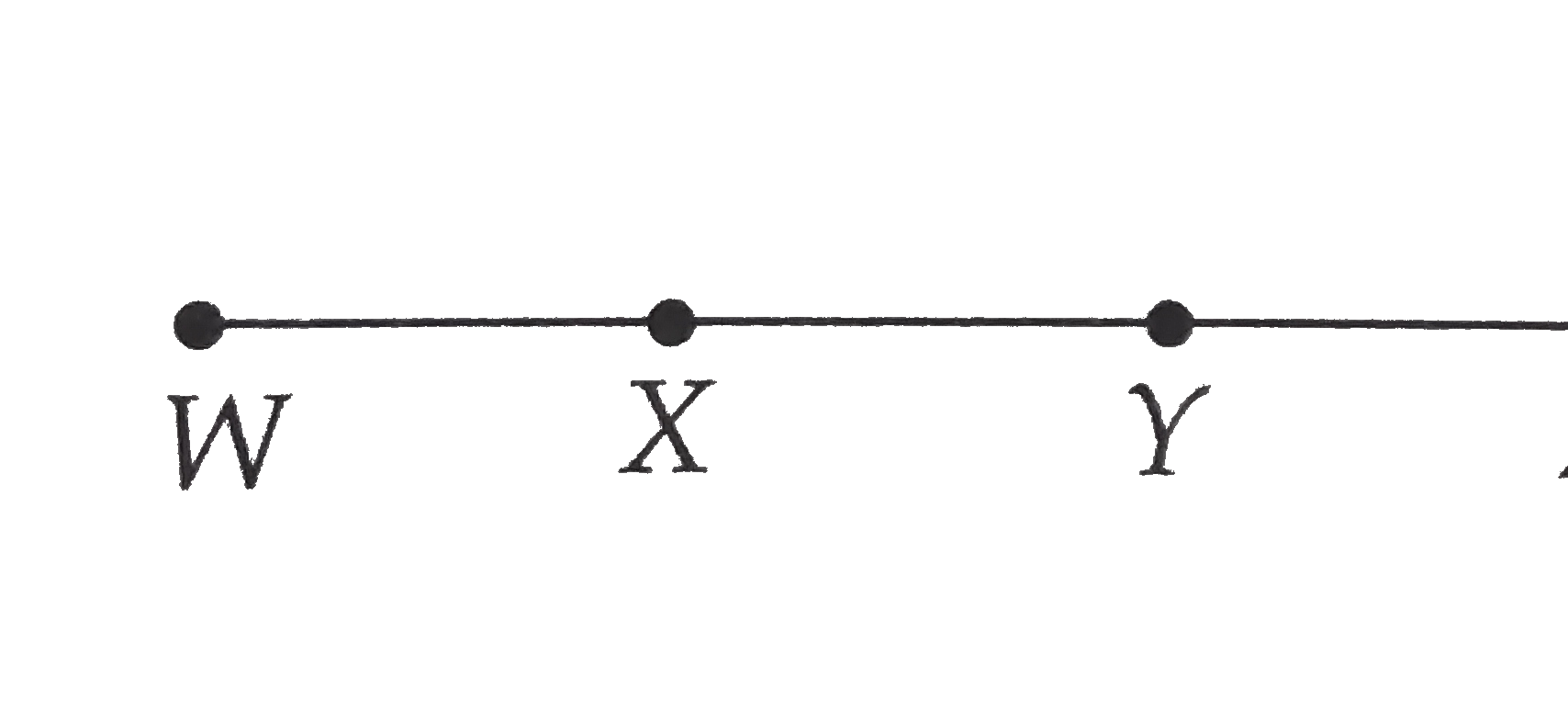
A, B, C, and D all lie on a number line. C is the midpoint of ¯¯¯¯¯¯AB and D is the midpoint of ¯¯¯¯¯¯AC.
Quantity AQuantity BThe ratio of ¯¯¯¯¯¯AD to ¯¯¯¯¯¯CBThe ratio of ¯¯¯¯¯¯AC to ¯¯¯¯¯¯AB
The correct Answer is:The two quantities are equal.
To solve the problem, we need to analyze the relationships between the points A, B, C, and D on a number line, where C is the midpoint of segment AB and D is the midpoint of segment AC. We will calculate the two quantities and compare them.
Step 1: Define the positions of A and B
Let's place point A at position 0 on the number line and point B at position 4x. This gives us a clear segment AB.
Step 2: Find the position of point C
Since C is the midpoint of segment AB, we can calculate its position as follows:
C=A+B2=0+4x2=2x
Step 3: Find the position of point D
D is the midpoint of segment AC. We need to find the position of D:
D=A+C2=0+2x2=x
Step 4: Calculate the lengths of segments
Now we can calculate the lengths of segments AD, CB, AC, and AB:
- Length of segment AD:
AD=D−A=x−0=x
- Length of segment CB:
CB=B−C=4x−2x=2x
- Length of segment AC:
AC=C−A=2x−0=2x
- Length of segment AB:
AB=B−A=4x−0=4x
Step 5: Calculate the ratios for Quantity A and Quantity B
- Quantity A: The ratio of AD to CB:
Quantity A=ADCB=x2x=12
- Quantity B: The ratio of AC to AB:
Quantity B=ACAB=2x4x=12
Step 6: Compare the two quantities
Both quantities are equal:
Quantity A=12,Quantity B=12
Conclusion
Since both quantities are equal, the answer is that the two quantities are equal.
Let's place point A at position 0 on the number line and point B at position 4x. This gives us a clear segment AB.
Since C is the midpoint of segment AB, we can calculate its position as follows:
C=A+B2=0+4x2=2x
D is the midpoint of segment AC. We need to find the position of D:
D=A+C2=0+2x2=x
Now we can calculate the lengths of segments AD, CB, AC, and AB:
- Length of segment AD:
AD=D−A=x−0=x
- Length of segment CB:
CB=B−C=4x−2x=2x
- Length of segment AC:
AC=C−A=2x−0=2x
- Length of segment AB:
AB=B−A=4x−0=4x
- Quantity A: The ratio of AD to CB:
Quantity A=ADCB=x2x=12
Quantity B=ACAB=2x4x=12
Both quantities are equal:
Quantity A=12,Quantity B=12
Since both quantities are equal, the answer is that the two quantities are equal.
Similar Questions
Knowledge Check
Point A, B, and C all lie on a line. Point D is midpoint of ¯¯¯¯¯¯AB and E is the midpoint of BC,¯¯¯¯¯¯AB=4and¯¯¯¯¯¯BC=10. Which of the following could be the length of ¯¯¯¯¯¯AE?
A1B2C3D4Quantity AQuantity B(0.¯7)(0.8)(35)(1.8)(15)(0.¯7)
AQuantity A is greater.BQuantity B is greater.CThe two quantities are equal.DThe relationship cannot be determined from the infromation given.0<p<q<r
Quantity AQuantity B q−p +q ¯¯¯¯¯¯¯¯¯¯¯2q−p(?)r−q -q¯¯¯¯¯¯¯¯¯¯¯r−2qAQuantity A is greater.BQuantity B is greater.CThe two quantities are equal.DThe relationship cannot be determined from the infromation given.
X, Y, and Z all lie on a number line. Segment ¯¯¯¯¯¯XY has a length of 5 and ¯¯¯¯¯¯YZ has a length of 7. If point U is the midpoint of ¯¯¯¯¯¯XZ,and¯¯¯¯¯¯UZ>2, what is the length of ¯¯¯¯¯¯UZ?
View SolutionThe length of ¯¯¯¯¯¯¯WZ is 3a+15, and the length of ¯¯¯¯¯¯¯WX is 7a+5. If Y is the midpoint of ¯¯¯¯¯¯XZ, what is the length of ¯¯¯¯¯¯¯WY ?
View SolutionIn the figure below, ABCD is a rectangle, EFGH is a square, and ¯¯¯¯¯¯CD is a diameter of a semicircle. Point K is the midpoint of ¯¯¯¯¯¯CD. Point J is the midpoint of both ¯¯¯¯¯¯AB and ¯¯¯¯¯¯EF. Points E and F lie on ¯¯¯¯¯¯AB. The 3 given lengths are in meters.
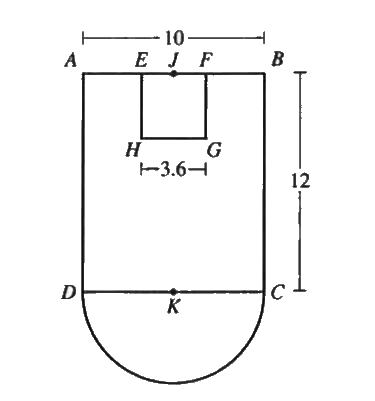
What is the length, in meters, of ¯¯¯¯¯¯JD?
View SolutionIn the figure below, ABCD is a rectangle, EFGH is a square, and ¯¯¯¯¯¯CD is a diameter of a semicircle. Point K is the midpoint of ¯¯¯¯¯¯CD. Point J is the midpoint of both ¯¯¯¯¯¯AB and ¯¯¯¯¯¯EF. Points E and F lie on ¯¯¯¯¯¯AB. The 3 given lengths are in meters.
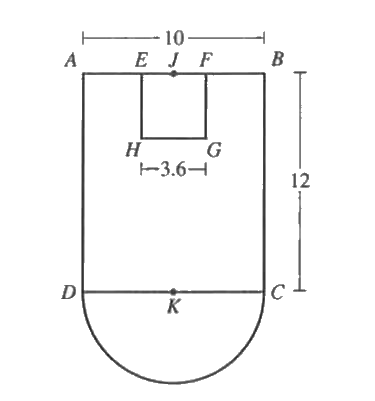
What is the length, in meters, of are ¯¯¯¯¯¯CD?
View SolutionIn the figure below, ABCD is a rectangle, EFGH is a square, and ¯¯¯¯¯¯CD is a diameter of a semicircle. Point K is the midpoint of ¯¯¯¯¯¯CD. Point J is the midpoint of both ¯¯¯¯¯¯AB and ¯¯¯¯¯¯EF. Points E and F lie on ¯¯¯¯¯¯AB. The 3 given lengths are in meters.
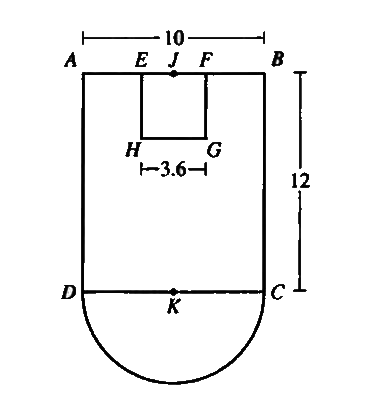
The length of ¯¯¯¯¯¯EH is what precent of the length of ¯¯¯¯¯¯AD?
View Solution