Point A, B, and C all lie on a line. Point D is midpoint of ¯¯¯¯¯¯AB and E is the midpoint of BC,¯¯¯¯¯¯AB=4and¯¯¯¯¯¯BC=10. Which of the following could be the length of ¯¯¯¯¯¯AE?
1
2
3
4
The correct Answer is:A
To solve the problem, we need to find the possible lengths of segment ¯AE given that points A, B, and C lie on a line, with D as the midpoint of ¯AB and E as the midpoint of ¯BC. The lengths of ¯AB and ¯BC are given as 4 and 10, respectively.
1. Define Points on a Number Line:
- Let point A be at position 0 on the number line.
- Since ¯AB=4, point B will be at position 4 (i.e., B=A+4=0+4=4).
- Now, we need to determine the position of point C. Since ¯BC=10, point C can be either to the right or left of point B.
2. Case 1: C is to the Right of B:
- If C is to the right of B, then C=B+10=4+10=14.
- Now, we find the midpoint E of ¯BC:
E=B+C2=4+142=182=9
- Now, we calculate the length of ¯AE:
¯AE=E−A=9−0=9
3. Case 2: C is to the Left of B:
- If C is to the left of B, then C=B−10=4−10=−6.
- Again, we find the midpoint E of ¯BC:
E=B+C2=4+(−6)2=−22=−1
- Now, we calculate the length of ¯AE:
¯AE=E−A=−1−0=−1(but we take absolute value, so 1)
4. Conclusion:
- From both cases, we find that the possible lengths of ¯AE are 9 (from Case 1) and 1 (from Case 2).
- Since the question asks for which of the following could be the length of ¯AE, we see that 1 is a valid option.
Final Answer:
The possible length of ¯AE is 1.
- Let point A be at position 0 on the number line.
- Since ¯AB=4, point B will be at position 4 (i.e., B=A+4=0+4=4).
- Now, we need to determine the position of point C. Since ¯BC=10, point C can be either to the right or left of point B.
- If C is to the right of B, then C=B+10=4+10=14.
- Now, we find the midpoint E of ¯BC:
E=B+C2=4+142=182=9
- Now, we calculate the length of ¯AE:
¯AE=E−A=9−0=9
- If C is to the left of B, then C=B−10=4−10=−6.
- Again, we find the midpoint E of ¯BC:
E=B+C2=4+(−6)2=−22=−1
- Now, we calculate the length of ¯AE:
¯AE=E−A=−1−0=−1(but we take absolute value, so 1)
- From both cases, we find that the possible lengths of ¯AE are 9 (from Case 1) and 1 (from Case 2).
- Since the question asks for which of the following could be the length of ¯AE, we see that 1 is a valid option.
The possible length of ¯AE is 1.
Similar Questions
Knowledge Check
In the figure below, ABCD is a rectangle, EFGH is a square, and ¯¯¯¯¯¯CD is a diameter of a semicircle. Point K is the midpoint of ¯¯¯¯¯¯CD. Point J is the midpoint of both ¯¯¯¯¯¯AB and ¯¯¯¯¯¯EF. Points E and F lie on ¯¯¯¯¯¯AB. The 3 given lengths are in meters.
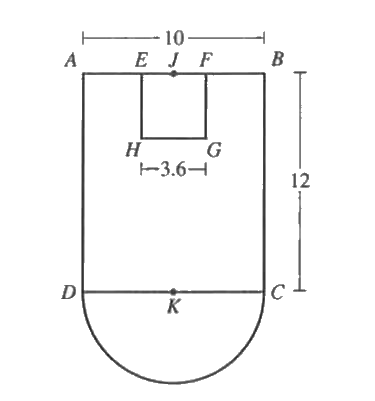
What is the length, in meters, of are ¯¯¯¯¯¯CD?A2.5πB5πC6.25πD10πIn the figure below, ABCD is a rectangle, EFGH is a square, and ¯¯¯¯¯¯CD is a diameter of a semicircle. Point K is the midpoint of ¯¯¯¯¯¯CD. Point J is the midpoint of both ¯¯¯¯¯¯AB and ¯¯¯¯¯¯EF. Points E and F lie on ¯¯¯¯¯¯AB. The 3 given lengths are in meters.
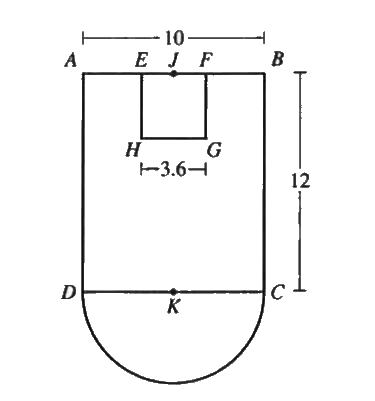
What is the length, in meters, of ¯¯¯¯¯¯JD?A13B15.6C17D√44In the figure below, ABCD is a rectangle, EFGH is a square, and ¯¯¯¯¯¯CD is a diameter of a semicircle. Point K is the midpoint of ¯¯¯¯¯¯CD. Point J is the midpoint of both ¯¯¯¯¯¯AB and ¯¯¯¯¯¯EF. Points E and F lie on ¯¯¯¯¯¯AB. The 3 given lengths are in meters.
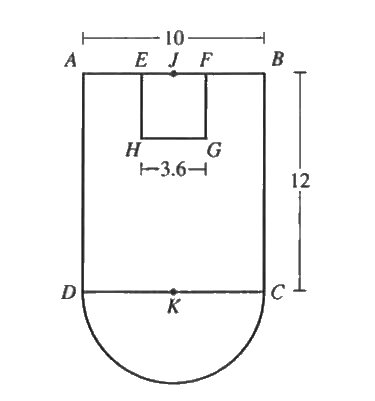
The figure will be placed in the standard (x,y) coordinate plane so that K is at the origin , ¯¯¯¯¯¯AB is parallel to the x-axis, and 1 meter equal 1 coordinates unit. Which of the following values could be the y-coordinate of H?A1.8B3.6C8.4D10
X, Y, and Z all lie on a number line. Segment ¯¯¯¯¯¯XY has a length of 5 and ¯¯¯¯¯¯YZ has a length of 7. If point U is the midpoint of ¯¯¯¯¯¯XZ,and¯¯¯¯¯¯UZ>2, what is the length of ¯¯¯¯¯¯UZ?
View SolutionIn triangle ABC,D is the midpoint of AB, E is the midpoint of DB and F is the midpoint of BC. If the area of ΔABC is 96, the area of ΔAEF is
View SolutionIn the figure below, ABCD is a rectangle, EFGH is a square, and ¯¯¯¯¯¯CD is a diameter of a semicircle. Point K is the midpoint of ¯¯¯¯¯¯CD. Point J is the midpoint of both ¯¯¯¯¯¯AB and ¯¯¯¯¯¯EF. Points E and F lie on ¯¯¯¯¯¯AB. The 3 given lengths are in meters.
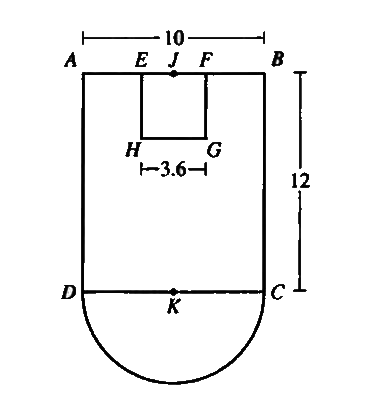
The length of ¯¯¯¯¯¯EH is what precent of the length of ¯¯¯¯¯¯AD?
View SolutionThe points P,Q,R and S lie in that order on a straight line . The midpoint of ¯¯¯¯¯¯QS is R and the midpoint of ¯¯¯¯¯PS is Q . The length of ¯¯¯¯¯¯QR is x feet and the length of ¯¯¯¯¯¯PQ is 4x−16 feet . What is the length , in feet , of ¯¯¯¯¯PS?
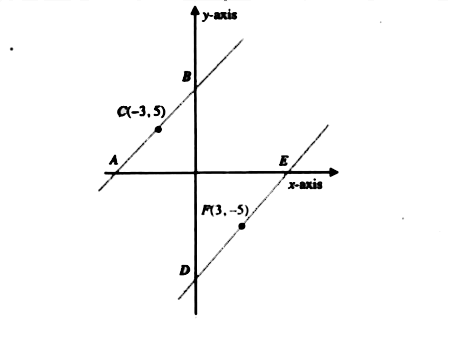
View SolutionColumn AIn the rectangular coordinate system shown, points A and E lie on the x-axis, and points B and D lie on the y-axis. Point C is the midpoint of the line AB and point F is the midpoint of the line DEColumn BThe slope of the line ABThe slope of the line DE
View Solution

