A line perpendicular to the line segment joining the points (1, 0) and (2, 3) divides it in the ratio 1:n. Find the equation of the line.
According to the section formula, the coordinates of the points that divides the line segment joining the points (1,0) and (2,3) in the ratio 1:n is given by
{n(1)+1(2)1+n,n(0)+1(3)1+n}={n+2n+1,3n+1}
The slope of the line joining the points (1,0) and (2,3) is m=3−02−1=3
We know that two non vertical lines are perpendicular to each other if and only if their slopes are negative reciprocals of each other.
Therefore, slope of the line that is perpendicular to the line joining the points (1,0) and (2,3) is =−1m=−13
Now the equation of the line passing through ={n+2n+1,3n+1} and whose slope is −13 is given by, {y−3n+1}=−13{x−n+2n+1}
⇒3[(n+1)y−3]=−[x(n+1)−(n+2)]
⇒3(n+1)y−9=−(n+1)x+n+2
⇒(1+n)x+3(1+n)y=n+11
Topper's Solved these Questions
- BOOK - NCERT ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE 10.52videos
STRAIGHT LINES
- BOOK - NCERT ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE 10.44videos
STRAIGHT LINES
- BOOK - NCERT ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE 10.114videos
STRAIGHT LINES
- BOOK - NCERT ENGLISHCHAPTER - STATISTICSEXERCISE - EXERCISE 15.210videos
STATISTICS
- BOOK - NCERT ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONSEXERCISE - All Questions110videos
TRIGONOMETRIC FUNCTIONS
Similar Questions
A line perpendicular to the in segment joining the points (1,0) and (2,3) divides it in the ratio 1:n . Find the equation of the line.
View SolutionIn which ratio the line segment joining the points (3, 0, 5) and (-2, 3, 2) is divided by YZ-plane?
View SolutionFind the equation of perpendicular bisector of line segment joining the points (1,5) and (3,−1)
View SolutionFind the ratio in which the line segment joining of the points (1,2) and (−2,3) is divided by the line 3x+4y=7
View SolutionFind the equation of the perpendicular bisector of the line segment joining the points (1,1) and (2,3).
View SolutionXY plane divides the line segment joining the points (1,2,-3) and (0,1,5) in the ratio __________
View SolutionFind the equation of the perpendicular bisector of the line segment joining the points (1,0) and (3,5).
View SolutionM is the mid-point of the line segment joining the points A(0, 4) and B(6, 0). M also divides the line segment OP in the ratio 1:3. Find :
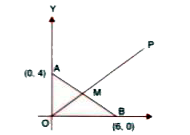
length of BPView SolutionFind the ratio in which the line segment joining the points (–3,10) and (6,–8) is divided by (–1,6).
View SolutionThe point which divides the line segment joining the points (8,–9) and (2,3) in ratio 1 : 2 internally lies in the
View Solution
