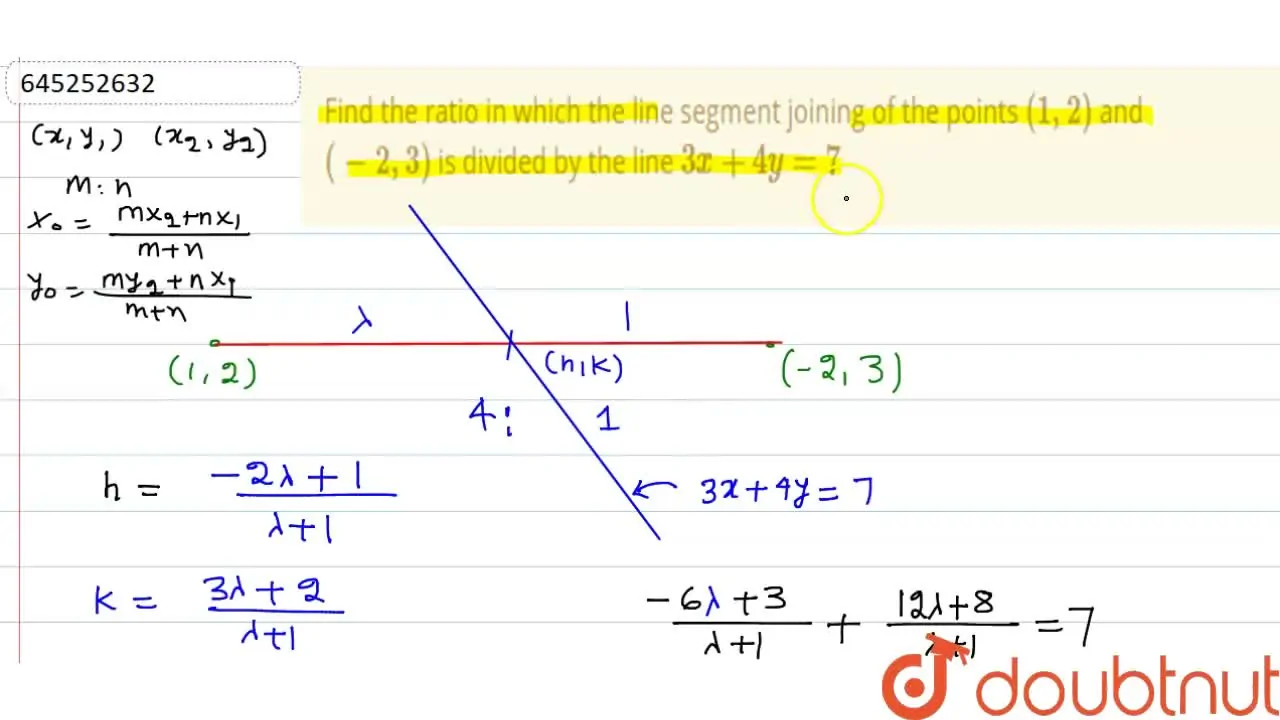
Find the ratio in which the line segment joining of the points (1,2) and (−2,3) is divided by the line 3x+4y=7
Step by step video & image solution for Find the ratio in which the line segment joining of the points (1, 2) and (-2, 3) is divided by the line 3x + 4y =7 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Find the ratio in which the line segment joining the points (2, -1, 3) and (-1, 2, 1) is divided by the plane x + y + z = 5.
View SolutionFind the ratio in which the line segment joining the points (2,-1,3) and (-1,2,1) is divided by the plane x+y+z=5.
View SolutionFind the ratio in which the line segment joining the points (2,4,5) and (3,-5,4) is divide by the yz-plane.
View SolutionFind the ratio in which the line segment joining the points (–3,10) and (6,–8) is divided by (–1,6).
View SolutionThe ratio in which the line segment joining the points (−2,4,5)and(3,5,−4) is divided by the yz-plane is
View SolutionWrite the ratio in which the line segment joining points (2, 3) and (3, −2) is divided by X axis.
View SolutionThe ratio in which the line segment joining the points (2,4,−3)and(−3,5,4) divided by XY-plane is
View SolutionFind the ratio in which Y-axis divides the line segment joining the points (3, 4) and (-2, 5).
View SolutionCalculate the ratio in which the line joining the points (-3, -1) and (5, 7) is divided by the line x = 2.
View SolutionFind the ratio in which the line joining the points (2, 3, 5) and (3, 4, 1) is divided by the plane
x−2y+z=5.View Solution