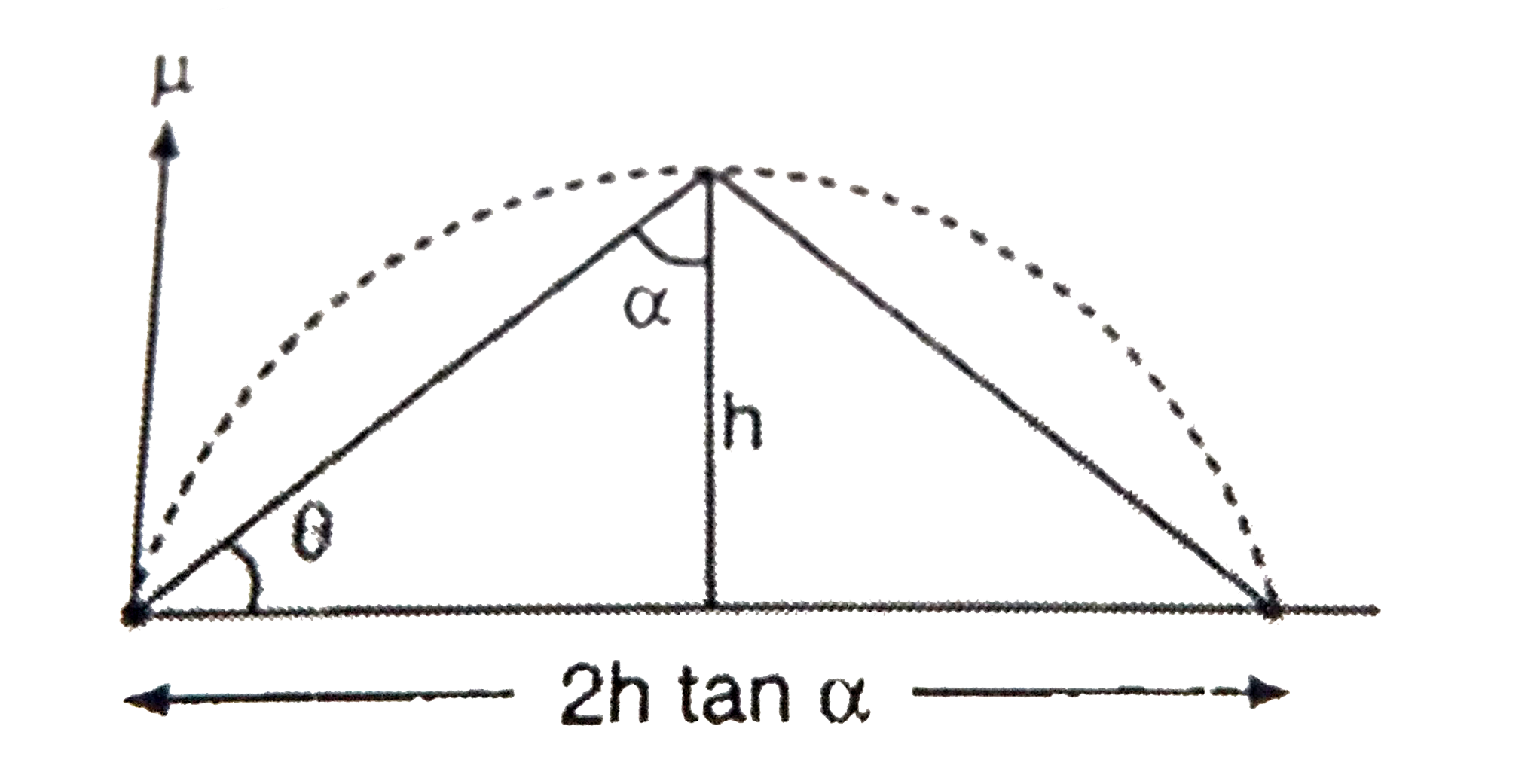
A particle is thrown over a triangle from one end of a horizontal base and grazing the vertex falls on the other end of the base. If α and β be the base angles and θ be the angle of projection, prove that tan θ=tanα+tanβ Solution in Telugu
The situation is shown in figure. From figure, we have

tanα+tanβ=yx+yR−x,tanα+tanβ=yRx(R−x)…(i)
But equation of trajectory is Y=xtanθ[1−xR]
tanθ=yRx(R−x)...(ii)
From Eqs. (i) and (ii), tanθ=tanα+tanβ
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - SHORT ANSWER TYPE QUESTIONS
6 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
10 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-3 (Circular Motion)
7 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question
15 Videos
Similar Questions
Show that the trajectory of an object thrown at certain angle with the horizontal is a parabola .
View SolutionWhat is the acceleration of a projectile at the top of its trajectory ?
View SolutionA particle ‘P is moving in a circle of radius "r" with uniform speed v. AB is the diameter of circle and 'C' is the centre. The angular velocity of P about A and C are in the ratio.
View SolutionGive two examples of the motion of big objects where the object can be treated as a particle and where it cannot be?
View SolutionA particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If alpha and beta be the base angles and theta the angle of projection, prove that tan theta = tan alpha + tan beta .
View SolutionA particle is projected over a triangle from one extremity of its horizontal base. Grazing over the vertex, it falls on the other extremity of the base. If a and b are the base angles of the triangle and theta the angle of projection, prove that tan theta = tan prop + tan beta .
View SolutionA particle is projected over a traingle from one end of a horizontal base and grazing the vertex falls on the other end of the base. If alpha and beta be the base angles and theta the angle of projection, prove that tan theta = tan alpha + tan beta .
View SolutionA projectile is fired from the base of cone shaped hill. The projectle grazes the vertex and strikes the hill again at the base. If α be the half-angle of the cone, h its height, u the initial velocity of projection and θ angle of projection, then tanθtanα is:
View SolutionA particle is projected up an inclines plane. Plane is inclined at an angle theta with horizontal and particle is projected at an angle alpha with horizontal. If particle strikes the plane horizontally prove that tan alpha=2 tan theta
View SolutionA particle thrown over a triangle from one end of a horizontal base falls on the other end of the base after grazing the vertex. If alpha and beta are the base angles of triangle and angle of projection is theta , then prove that ( tan theta = tan alpha + tan beta)
View SolutionA particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If 30^(@) and 60^(@) be the base angles and theta the angle of projection then tan theta is
View SolutionA particle is projected over a triangle from one end of a horizontal base and garzing the vertex falls on the other end of the base . If α and β the base angles and θ the angle of projection then show that tanθ=tanα+tanβ.
View SolutionA particle is thrown over a triangle from one end of a horizontal base and grazing the vertex falls on the other end of the base. If α and β be the base angles and θ be the angle of projection, prove that tan θ=tanα+tanβ
View SolutionA particle is thrown over a triangle from one end of a horizontal base and grazing the vertex falls on the other end of the base. If α and β be the base angles and θ be the angle of projection, prove that tanθ=tanα+tanβ.
View SolutionA particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If αandβ be the base angles and θ the angle of projection, prove that tanθ=tanα+tanβ .
View Solution
