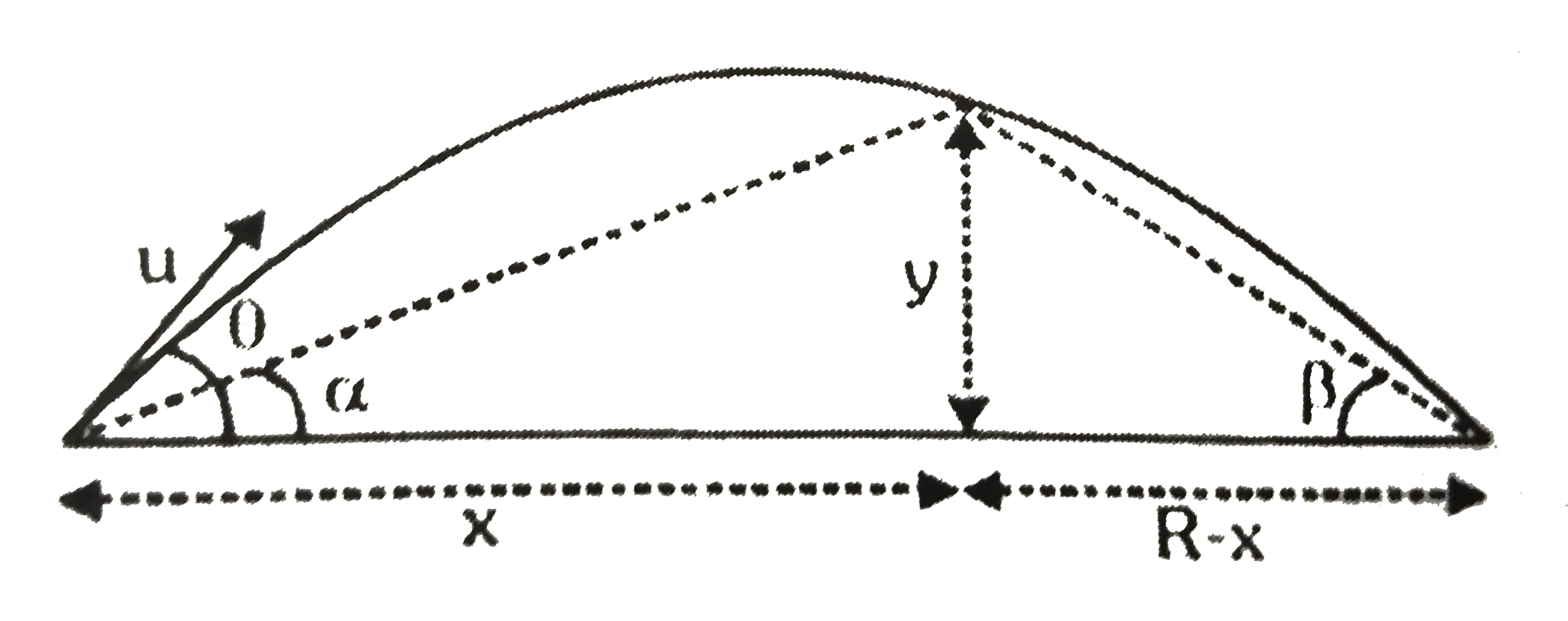
A particle thrown over a triangle from one end of a horizontal base falls on the other end of the base after grazing the vertex. If $α and β$ are the base angles of triangle and angle of projection is $θ$ , then prove that $(tan θ = tan α + tan β)$

Video Solution

Text Solution

Verified by Experts

From triangle $y = x tan α and y = (R - x) tan β$
$tan α + tan β = \frac{y}{x} + \frac{y}{R - x} = \frac{y R}{x (R - x)}$
$∵ y = x tan θ [1 - \frac{x}{R}] \Rightarrow tan θ = \frac{y R}{x (R - x)}$
$∴ tan θ = tan α + tan β$

|

Updated on:21/07/2023

Class 11 PHYSICS RECTILINEAR MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A particle is thrown over a triangle from one end of horizontal base and grazing over the vertex falls on the other end of the base. If $α, β$ are the base angles and $θ$ the angle of projection, then
A $tan θ = tan α - tan β$
B $tan θ = tan β - tan α$
C $tan θ = tan α + tan β$
DNone of these
Question 2 - Select One
A particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If $30^{\circ} and 60^{\circ}$ be the base angles and $θ$ the angle of projection then $tan θ$ is
A $\frac{2}{\sqrt{3}}$
B $\frac{4}{\sqrt{3}}$
C $\frac{1}{3}$
D3
Question 3 - Select One
If $α$ and $β$ are acute such that $α + β$ and $α - β$ satisfy the equation ${tan}^{2} θ - 4 tan θ + 1 = 0$ , then $(α, β$ ) =
A $(30^{\circ}, 60^{\circ})$
B $(45^{\circ}, 45^{\circ})$
C $(45^{\circ}, 30^{\circ})$
D $(60^{\circ}, 45^{\circ})$

ALLEN-KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)-BEGINNER S BOX-7

Home
Ask Doubt
Profile