A body projected from the ground reaches a point 'X' in its path after 3 seconds and from there it reaches the ground after further 6 seconds. The vertical distance of the point 'X' from the ground is (acceleration due to gravity =10ms−2)Solution in Telugu
30m
60m
80m
90m
The correct Answer is:D
Step by step video & text solution for A body projected from the ground reaches a point 'X' in its path after 3 seconds and from there it reaches the ground after further 6 seconds. The vertical distance of the point 'X' from the ground is (acceleration due to gravity =10ms^(-2)) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE Book:AAKASH SERIESChapter:MOTION IN A STRAIGHT LINE Exercise:PRACTICE EXERCISE
Explore 58 Videos
- MOTION IN A STRAIGHT LINE Book:AAKASH SERIESChapter:MOTION IN A STRAIGHT LINE Exercise:problems
Explore 47 Videos
- MOTION IN A STRAIGHT LINE Book:AAKASH SERIESChapter:MOTION IN A STRAIGHT LINE Exercise:EXERCISE -I
Explore 58 Videos
- MOTION IN A PLANEBook:AAKASH SERIESChapter:MOTION IN A PLANEExercise:QUESTION FOR DESCRIPTIVE ANSWER
Explore 7 Videos
- MOVING CHARGES AND MAGNETISMBook:AAKASH SERIESChapter:MOVING CHARGES AND MAGNETISMExercise:EXERCISE-III
Explore 45 Videos
Similar Questions
If a cyclist takes two minutes to compete half revolution on a circular path of 120 m radius. What is the average speed?
View SolutionFind the covered by the particles,in the following figures,(i) and (ii) while a particle travels from A to B as shown by the arrows.
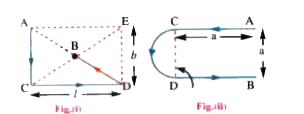
View SolutionThe ratio of the numerical values of the average velocity and average speed of a body is always
View SolutionA particle is projected over a triangle from one end of a horizontal base and garzing the vertex falls on the other end of the base . If α and β the base angles and θ the angle of projection then show that tanθ=tanα+tanβ.
View SolutionA proton, a deuteron and an a particle having same momentum enter a uniform magnetic field at right angles to the field. Then the ratio of their angular momenta during their motion in the magnetic field is
View SolutionA stone projected vertically up from the ground reaches a height y in its path at t1 seconds and after further t2 seconds reaches the ground. The height y is equal to
View SolutionA body projected vertically upwords from the top of a tower reaches the ground in t1 second . If it projected vertically downwards from the some top with same velocity ,it reaches the ground in t2seconds . If it is just dropped from the top it reaches the ground in t second .prove that t=√t1t2
View SolutionA body projected from the ground reaches a point 'X' in its path after 3 seconds and from there it reaches the ground after further 6 seconds. The vertical distance of the point 'X' from the ground is (acceleration due to gravity =10ms−2)
View SolutionA body projected up reaches a point A in its path at the end of 4th second and reaches the ground after 5 seconds from the start. The height of A above the ground is (g=10m/s2)
View SolutionA stone projected vertically up from the ground reaches a height y in its path at t_1 seconds and after further t_2 seconds reaches the ground. The height y is equal to
View SolutionA body projected up reaches a point A in its path at the end of 4^(th) second and reaches the ground after 5 seconds from the starts .The height of A above the ground is (g=10 m//s^(2))
View SolutionA bullet fired vertically up from the ground reaches a height 40 m in its path from the ground and it takes further time 2 seconds to reach the same point during descent.The toatl time of flight is
View SolutionWhat is the area under the velocity-time curve in the case of a body projected vertically upwards from the ground after reaching the ground ?
View SolutionA body projected up reaches a point A in its path at the end of 4th second and reaches the ground after 5 seconds from the start. The height of A above the ground is (g=10ms2)
View SolutionA stone projected vertically up from the ground reaches a height y in its path at t1 seconds and after further t2 seconds reaches the ground. The height y is equal to
View Solution

