(a) State Kirchhoff's rules for an electirc network. Using Kirchhoff's rules, obtain the balance condition in terms of the resistances of four arms of Wheatstone bridge.
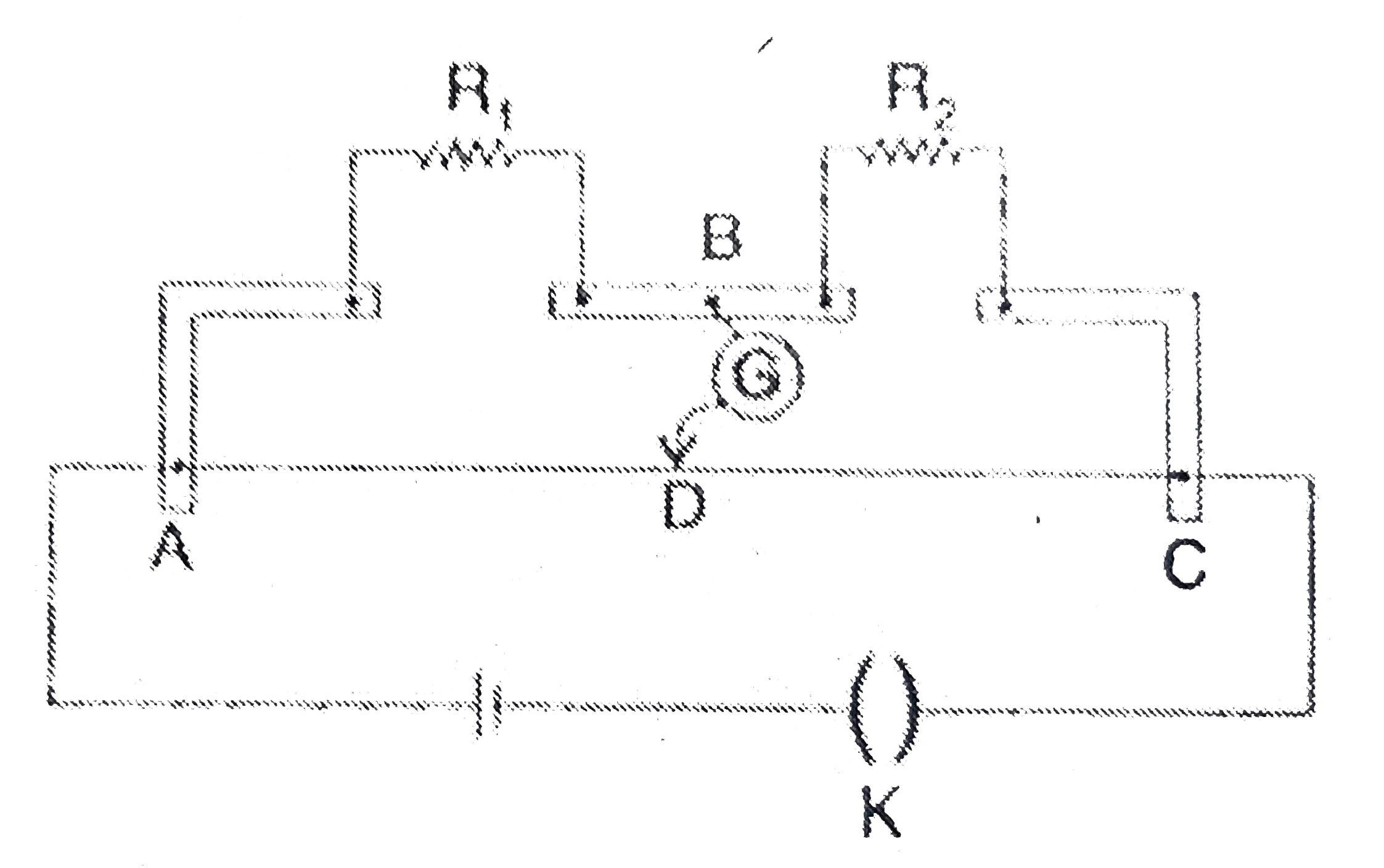
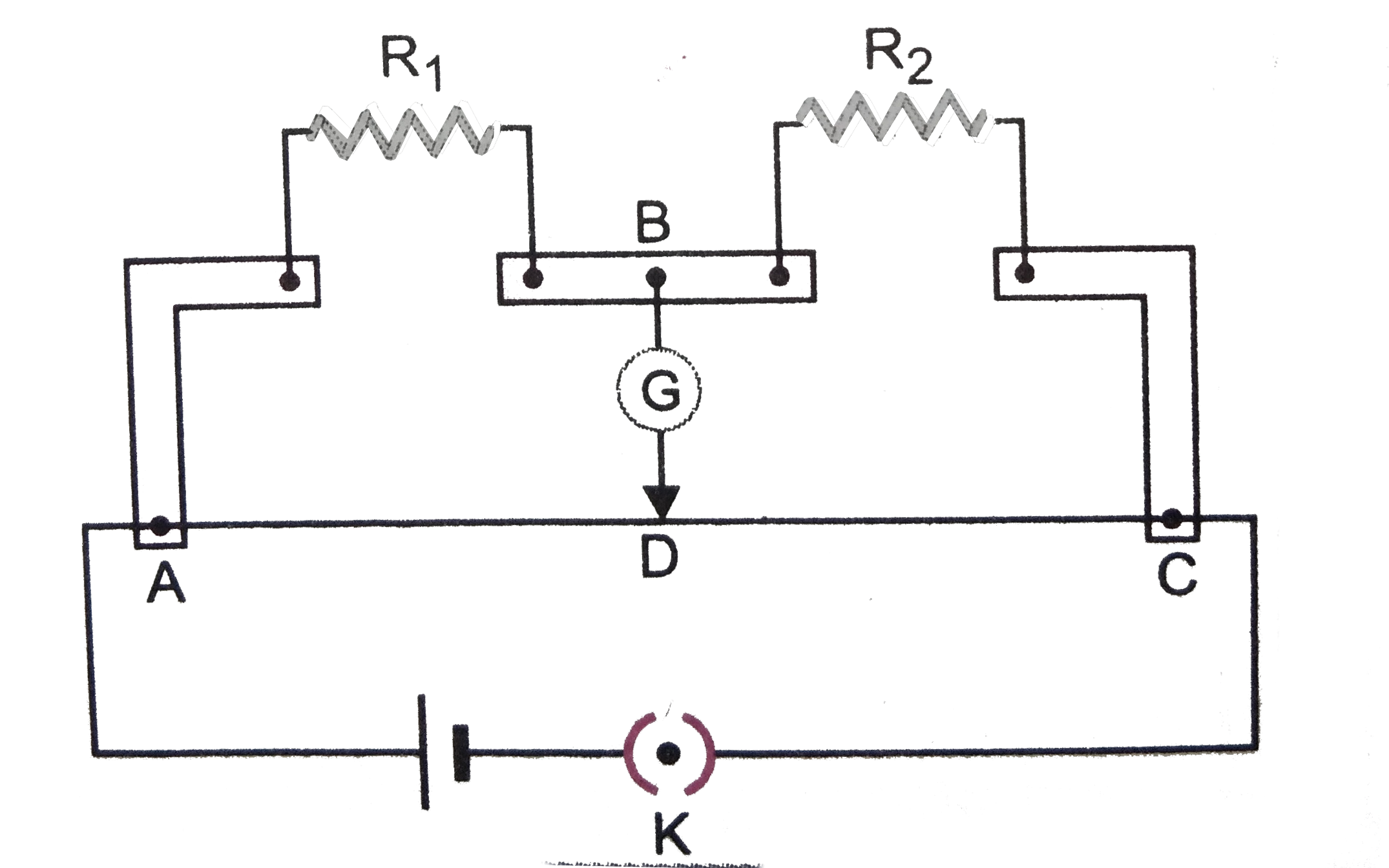
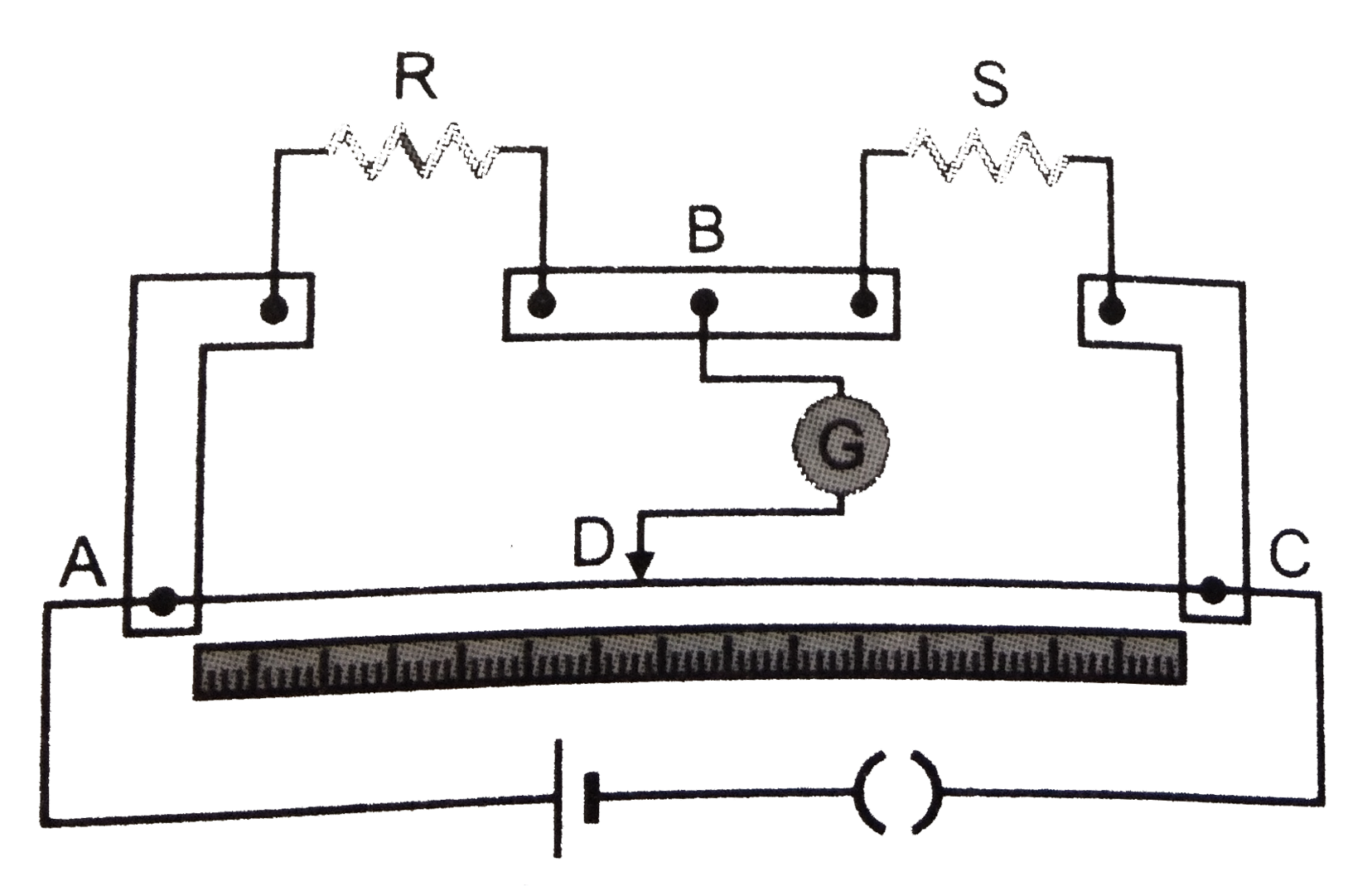
(b) In the meter bridge experimental set up, shown in the figure, the null point 'D' is obtained at a distance of 40 cm from end A of the meter bridge wire. If a resistance of $10 Ω$ is connected in series with $R_{1},$ null point is obtained at $A D = 60 c m .$ Calculate the values of $R_{1} and R_{2} .$

Video Solution

Text Solution

Verified by Experts

(a) Kirchhoff's First Law - junction Rule. The algebraic sum of the currents meeting at a point in an electrical circuit is always zero.
Let the currents be $I_{1}, I_{2}, I_{3} and I_{4} .$

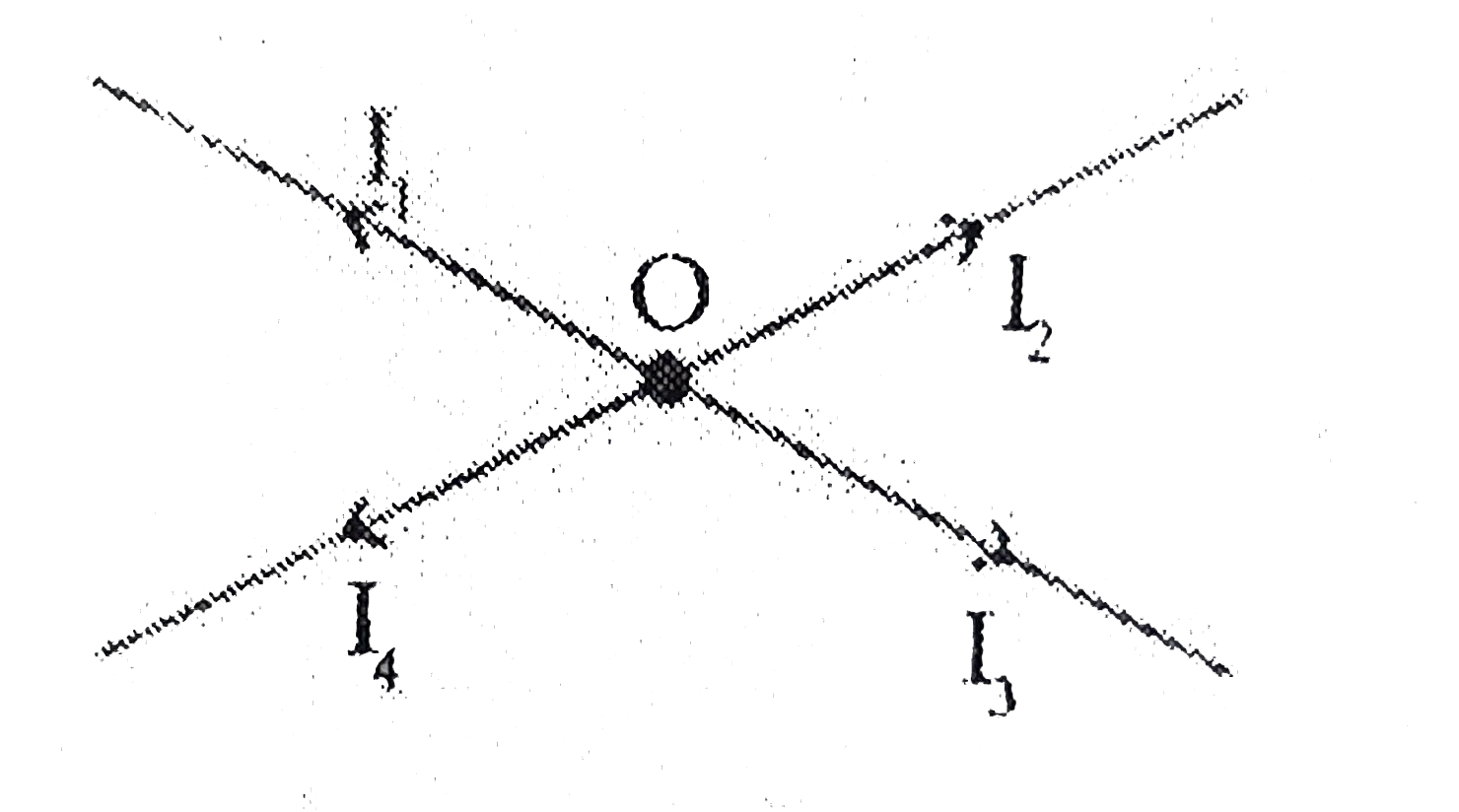
Convention : Current towards the junction -positive Current always from the junction-negative
$I_{3} + (- I_{1}) + (- I_{2}) + (- I_{4}) = 0$
Kirchhoff's Second Law -Loop Rule.
In a closed loop, the algebric sum of the emf's is equal to the algebric sum of the products of the resistances and current flowing through them.
For closed part $B A C B, E_{1} - E_{2} - I_{1} R_{1} + I_{2} R_{2} - I_{3} R_{3}$
For closed part $C A D C, E_{2} = I_{3} R_{3} + I_{4} R_{4} + I_{5} R_{5}$

Wheatstone Bridge : The Wheatstone Bridge is an arrangement of four resistance as shown in the following figure.
$R_{1}, R_{2}, R_{3} and R_{4}$ are the four resistances.
Galvanometer (a) has a current $I_{g}$ flowing through it at balanced condition,
$I_{g} = 0$
Applying junction rule at B,
$∴ I_{2} = I_{4}$
Applying junction rule at D.
$∴ I_{1} = I_{3}$
Applying loop rule to closed loop ADBA,
$- I_{1} R_{1} + O + I_{2} R_{2} = O$
$∴ \frac{I_{1}}{I_{2}} = \frac{R_{2}}{R_{1}}$ ...(i)
Applying loop rule to closed loop CBDC,
$I_{2} R_{4} + O - I_{1} R_{3} = O$ ...(ii).
From equations (i) and (ii)
$\frac{R_{2}}{R_{1}} = \frac{R_{4}}{R_{3}}$

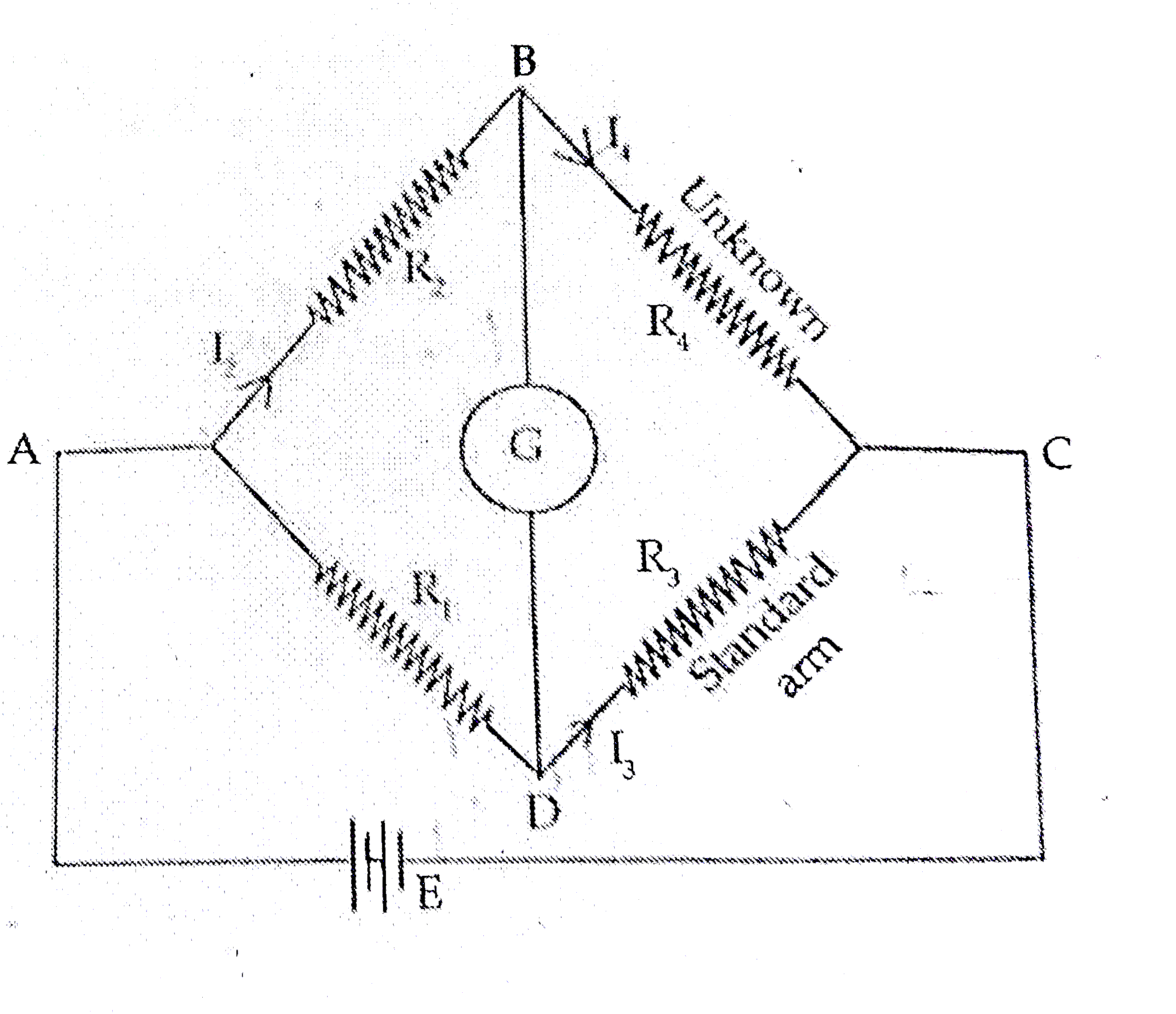
This is the required balanced condition of Wheatstone bridge.
(b) Considering both the situations and writing them in the form of equations.
Let R be the resistance per unit length of the potential meter wire,
$\frac{R_{1}}{R_{2}} = \frac{R' \times 40}{R' (100 - 40)} = \frac{40}{60} = \frac{2}{3} \Rightarrow \frac{R_{1} + 10}{R_{2}} = \frac{R' \times 60}{R' (100 - 60)} = \frac{60}{40} = \frac{3}{2}$
$\frac{R_{1}}{R_{2}} = \frac{2}{3}$ ...(i)
$\Rightarrow \frac{R_{1} + 10}{R_{2}} = \frac{3}{2}$ ...(ii)
Putting the value of $R_{1},$ from equation (i) subtracting in equation (ii)
$\frac{2}{3} + \frac{10}{R_{2}} = \frac{3}{2}$
$R_{2} = 12 Ω$
Recalling equation (i), again
$\frac{R_{1}}{1^{2}} = \frac{2}{3}$
$R_{1} = 8 Ω .$

Updated on:21/07/2023

|

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

In a meter bridge, the null point is found at a distance of 40 cm from A. If now a resistance of 12 $Ω$ is connected in parallel with S, the null point occurs at 60 cm from A. Determine the value of R.

A $15 Ω$
B $12 Ω$
C $10 Ω$
D $5 Ω$

XII BOARDS PREVIOUS YEAR-XII BOARDS-SET - I

Home
Ask Doubt
Profile