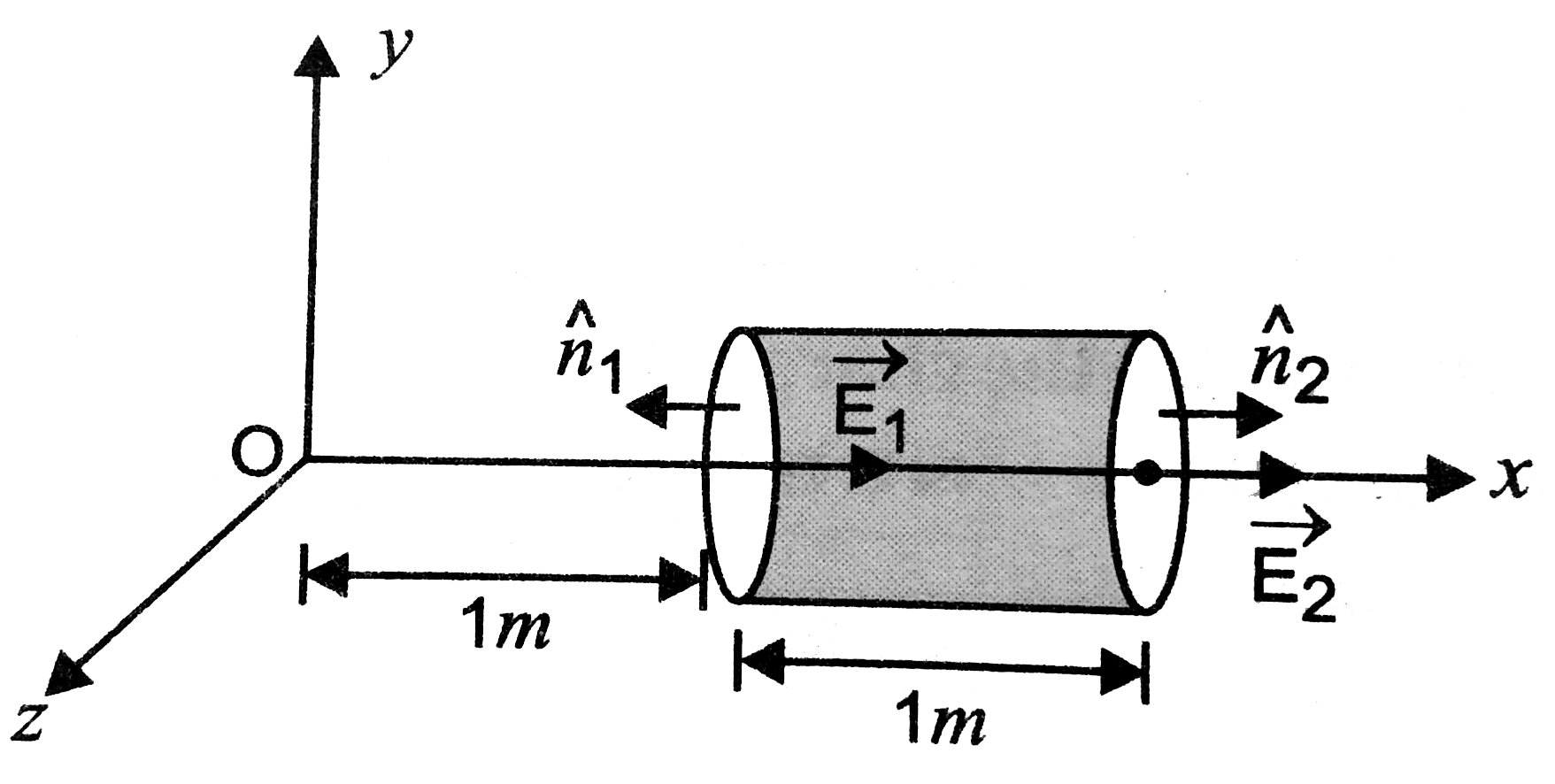
A hollow cylindrical box of length 1m and area of cross section $25 c m^{2}$ is placed in a three dimensional co-ordinate system as shown in Fig, The electric field in the
region is given by $\vec{E} = 50 x \hat{i}$ , where E is in $N C^{- 1}$ and x is in meter. Find
(i) Net flux through the cylinder
(ii) Charge enclosed by the cylinder.

Video Solution

Text Solution

Verified by Experts

Given $\vec{E} = 50 x \hat{I} and Δ s = 25 c m^{2} = 25 \times 10^{- 4} m^{2}$
As the electric field is only along the x - axis, so flux will pass only through the cross - section of cylinder.

Magnitude of electric field at cross - section A,
$E_{A} = 50 \times 1 = 50 N C^{- 1}$
Magnitude of electric field at cross - section B,
$E_{B} = 50 \times 2 = 100 N C^{- 1}$
The corresponding electric fluxes are :
$ϕ_{A} = \vec{E} \cdot \vec{Δ s} = 50 \times 25 \times 10^{- 4} \times {\cos 180}^{\circ} = - 0.125 N m^{2} / C$
$ϕ_{B} = \vec{E} \cdot \vec{Δ s} = 100 \times 25 \times 10^{- 4} \times {\cos 0}^{\circ} = 0.25 N m^{2} / C$
So, the net flux through the cylinder,
$ϕ = ϕ_{A} + ϕ_{B} = - 0.125 + 0.25 = 0.125 N m^{2} / C$
(ii) Using Gauss's Law:
$\oint \vec{E} . \vec{d s} = \frac{q}{ε_{0}} \Rightarrow 0.125$
$= \frac{q}{8.85 \times 10^{- 12}}$
$q = 8.85 \times 0.125 \times 10^{- 12} = 1.1 \times 10^{12} C .$

Updated on:21/07/2023