Use Kirchhoff s rules to obtain conditions for the balance condition in a Wheatstone bridge.
To derive the balance condition in a Wheatstone bridge using Kirchhoff's rules, we will follow these steps:
Step 1: Understand the Wheatstone Bridge Configuration
A Wheatstone bridge consists of four resistors arranged in a diamond shape. Let the resistors be:
- P (connected between points A and B)
- Q (connected between points B and C)
- R (connected between points D and A)
- S (connected between points D and C)
The galvanometer (G) is connected between the junctions B and D.
Step 2: Apply Kirchhoff's Current Law (KCL)
At junction B, according to KCL, the sum of currents entering a junction is equal to the sum of currents leaving the junction. Let:
- I1 be the current through resistor P
- I2 be the current through resistor Q
- Ig be the current through the galvanometer
- I3 be the current through resistor R
- I4 be the current through resistor S
From KCL at junction B:
I1=Ig+I3(Equation 1)
At junction D, applying KCL gives:
I2+Ig=I4(Equation 2)
Step 3: Consider the Balance Condition
For the bridge to be balanced, the current through the galvanometer (Ig) must be zero:
Ig=0
Substituting Ig = 0 into Equations 1 and 2:
From Equation 1:
I1=I3
From Equation 2:
I2=I4
Step 4: Apply Kirchhoff's Voltage Law (KVL)
Now, we will apply Kirchhoff's Voltage Law around the loops in the Wheatstone bridge.
Loop 1 (A-B-D-A):
The voltage drop across P and the galvanometer must equal the voltage drop across R:
I1⋅P=I2⋅R(Equation 3)
Loop 2 (B-C-D-B):
The voltage drop across Q and the galvanometer must equal the voltage drop across S:
I3⋅Q=I4⋅S(Equation 4)
Step 5: Substitute the Conditions from KCL into KVL
Since we have established that:
- I1=I3
- I2=I4
We can substitute these into Equations 3 and 4:
From Equation 3:
I1⋅P=I2⋅R
From Equation 4:
I1⋅Q=I2⋅S
Step 6: Derive the Balance Condition
Now we can express the ratios:
From Equation 3:
PR=I2I1
From Equation 4:
QS=I2I1
Since both ratios are equal:
PR=QS
Thus, we arrive at the balance condition for the Wheatstone bridge:
PQ=RS
Conclusion
The condition for balance in a Wheatstone bridge is given by:
PQ=RS
A Wheatstone bridge consists of four resistors arranged in a diamond shape. Let the resistors be:
- P (connected between points A and B)
- Q (connected between points B and C)
- R (connected between points D and A)
- S (connected between points D and C)
At junction B, according to KCL, the sum of currents entering a junction is equal to the sum of currents leaving the junction. Let:
- I1 be the current through resistor P
- I2 be the current through resistor Q
- Ig be the current through the galvanometer
- I3 be the current through resistor R
- I4 be the current through resistor S
I1=Ig+I3(Equation 1)
I2+Ig=I4(Equation 2)
For the bridge to be balanced, the current through the galvanometer (Ig) must be zero:
Ig=0
From Equation 1:
I1=I3
I2=I4
Now, we will apply Kirchhoff's Voltage Law around the loops in the Wheatstone bridge.
The voltage drop across P and the galvanometer must equal the voltage drop across R:
I1⋅P=I2⋅R(Equation 3)
The voltage drop across Q and the galvanometer must equal the voltage drop across S:
I3⋅Q=I4⋅S(Equation 4)
Since we have established that:
- I1=I3
- I2=I4
From Equation 3:
I1⋅P=I2⋅R
I1⋅Q=I2⋅S
Now we can express the ratios:
From Equation 3:
PR=I2I1
QS=I2I1
PR=QS
PQ=RS
The condition for balance in a Wheatstone bridge is given by:
PQ=RS
Topper's Solved these Questions
- CBSE EXAMINATION PAPER, DELHI REGION - 2015 (CODE NO. 55/1/1/D)Book:CBSE COMPLEMENTARY MATERIALChapter:CBSE EXAMINATION PAPER, DELHI REGION - 2015 (CODE NO. 55/1/1/D)Exercise:SECTION C
Explore 15 Videos
- CBSE EXAMINATION PAPER, DELHI REGION - 2015 (CODE NO. 55/1/1/D)Book:CBSE COMPLEMENTARY MATERIALChapter:CBSE EXAMINATION PAPER, DELHI REGION - 2015 (CODE NO. 55/1/1/D)Exercise:SECTION E
Explore 6 Videos
- CBSE EXAMINATION PAPER, DELHI REGION - 2015 (CODE NO. 55/1/1/D)Book:CBSE COMPLEMENTARY MATERIALChapter:CBSE EXAMINATION PAPER, DELHI REGION - 2015 (CODE NO. 55/1/1/D)Exercise:SECTION E
Explore 6 Videos
- CBSE Examination Paper Delhi–2014Book:CBSE COMPLEMENTARY MATERIALChapter:CBSE Examination Paper Delhi–2014Exercise:SET-III (Questions Uncommon to set-I and II)
Explore 9 Videos
- DUAL NATURE OF MATTER AND RADIATION & ATOMS AND NUCLEIBook:CBSE COMPLEMENTARY MATERIALChapter:DUAL NATURE OF MATTER AND RADIATION & ATOMS AND NUCLEIExercise:Long Answer Question
Explore 22 Videos
Similar Questions
Knowledge Check
Figure 6.64 shows a balanced wheatstone bridge.
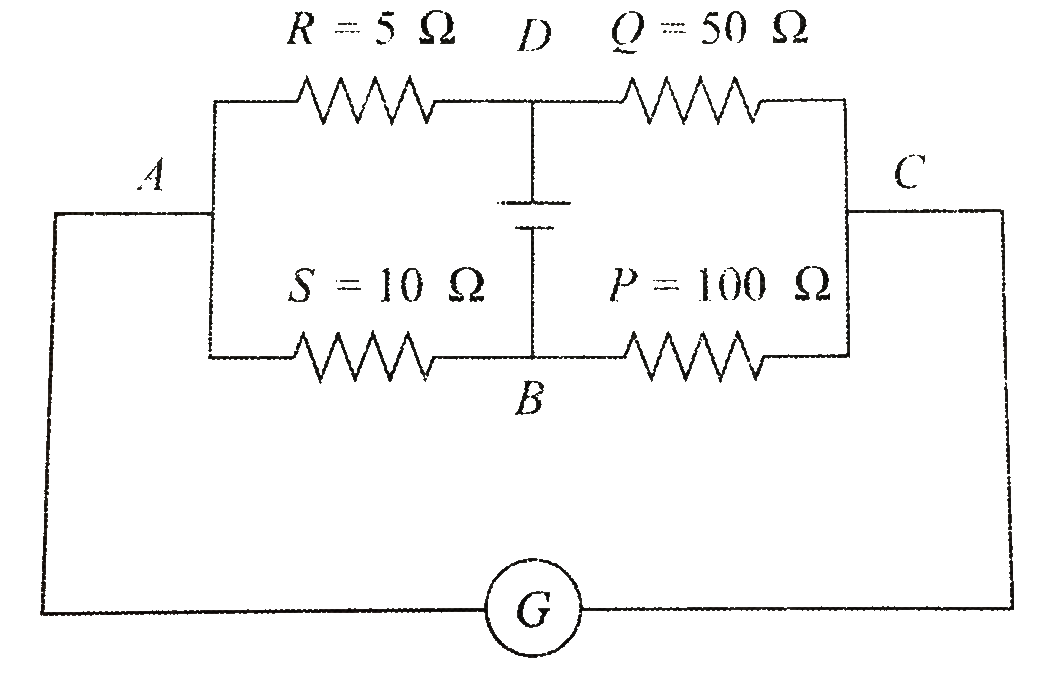 AIf Pis slightly increased, the current in the galvanometer flows from C to A.BIf Pis slightly increased, the current in the galvanometer flows from A to C.CIf Qis slightly increased, the current in the galvanometer flows from C to A.DIf Q is slightly increased, the current in the galvanometer flows from A to C.
AIf Pis slightly increased, the current in the galvanometer flows from C to A.BIf Pis slightly increased, the current in the galvanometer flows from A to C.CIf Qis slightly increased, the current in the galvanometer flows from C to A.DIf Q is slightly increased, the current in the galvanometer flows from A to C.Wheatstone bridge can be used
Ato compare two unknown resistances.Bto measure small strains produced in hardmetalCas the working principle of meterbridgeDall the aboveIncomnia condition is used by
AequanilBsacchrimCbithionalDamipicilln
Balanced Wheatstone Bridge
View Solution(a) State Kirchhoff's rules for an electirc network. Using Kirchhoff's rules, obtain the balance condition in terms of the resistances of four arms of Wheatstone bridge.
(b) In the meter bridge experimental set up, shown in the figure, the null point 'D' is obtained at a distance of 40 cm from end A of the meter bridge wire. If a resistance of 10Ω is connected in series with R1, null point is obtained at AD=60cm. Calculate the values of R1andR2.

View Solution(a) State Kirchhoff's rules for an electric network. Using Krichhoff's rules, obtain the balance condition in terms of the resistances of four arms of Wheatstone bridge,
(b) In the meterbridge experimental set up, shown in the Fig., the null point 'D' is obtained at a distance of 40 cm from end A of the meterbridge wire. If a resistance of 10Ω is connected in series with R1, null point is obtained at AD = 60 cm. Calculate the values of R1 and R2

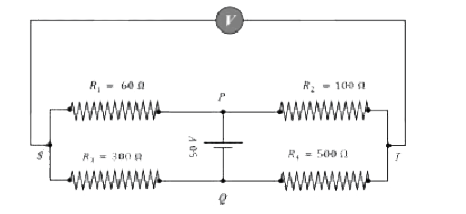
View SolutionIn the balanced condition , the values of the resistance of the fourarms of a Wheatstone bridge are shown in the figure below. The resistance R3 has temperature coefficinet 0.0004∘C−1. If the temperature of R3 increased by 100∘ C , the voltage developed between S and T will be _____volt.
View SolutionIn a wheatstone's bridge arrangement we can interchange the cell and galvanometer without affecting the balance condition of the bridge.
View Solution