In Fig 16-45, a string, tied to a sinusoidal oscillator at P and running over a support at Q, is strecthed by a block of mass m, Separation, L=1,20m,l linear density μ=1.20g/m, and the oscilator frequency f=120Hz. The amplitude of the motion at P is small enough for that point to be considered a node. A node also exists at Q. (a) What mass m allows the osciallator to set up the fourth harmonic on the string? (b) What standing wave mode, if any can be set up if m=1.00kg?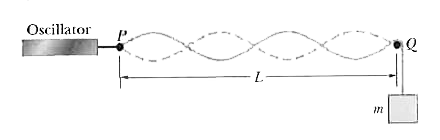 
The correct Answer is:(a) 0.635kg' (b) the mass cannot set up a standing wave on the string
Step by step video, text & image solution for In Fig 16-45, a string, tied to a sinusoidal oscillator at P and running over a support at Q, is strecthed by a block of mass m, Separation, L=1,20m,l linear density mu=1.20 g//m, and the oscilator frequency f=120Hz. The amplitude of the motion at P is small enough for that point to be considered a node. A node also exists at Q. (a) What mass m allows the osciallator to set up the fourth harmonic on the string? (b) What standing wave mode, if any can be set up if m=1.00kg? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Single Correct Choice Type)
33 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (More than One Coorect Choice Type)
10 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Checkpoint
8 Videos
- WAVE - IIBOOK - RESNICK AND HALLIDAYCHAPTER - WAVE - IIEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)
5 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (Integer Type)
5 Videos
Similar Questions
In Fig. 16-45, a string, tied to a sinusoidal oscillator at P and running over a support at Q, is stretched by a block of mass m. The separation L between P and Q is 1.20 m, and the frequency f of the oscillator is fixed at 120 Hz. The amplitude of the motion at P is small enough for that point to be considered a node. A node also exists at Q. A standing wave appears when the mass of the hanging block is 286.1 g or 4470g, but not for any intermediate mass. What is the linear density of the string?
View SolutionA string has linear density μ=525g/m and is under tension τ=45N. We send a sinusoidal wave with frequency f=120Hz and amplitude ym=8.5 mm along the string. At what average rate does the wave transport energy?
View Solution
Knowledge Check
The linear mass density μ of the string is (where, mass of the string = m, length, of the string g = L)
AmLBmLCmL2DmL3The linear mass density 'μ' of the string is (where, mass of the string = m, length of the string = L)
AmLBmLCmt2DmL3The mass M shown in the figure oscillates in simple harmnonic motion and amplitude A. The amplitude of the point P is
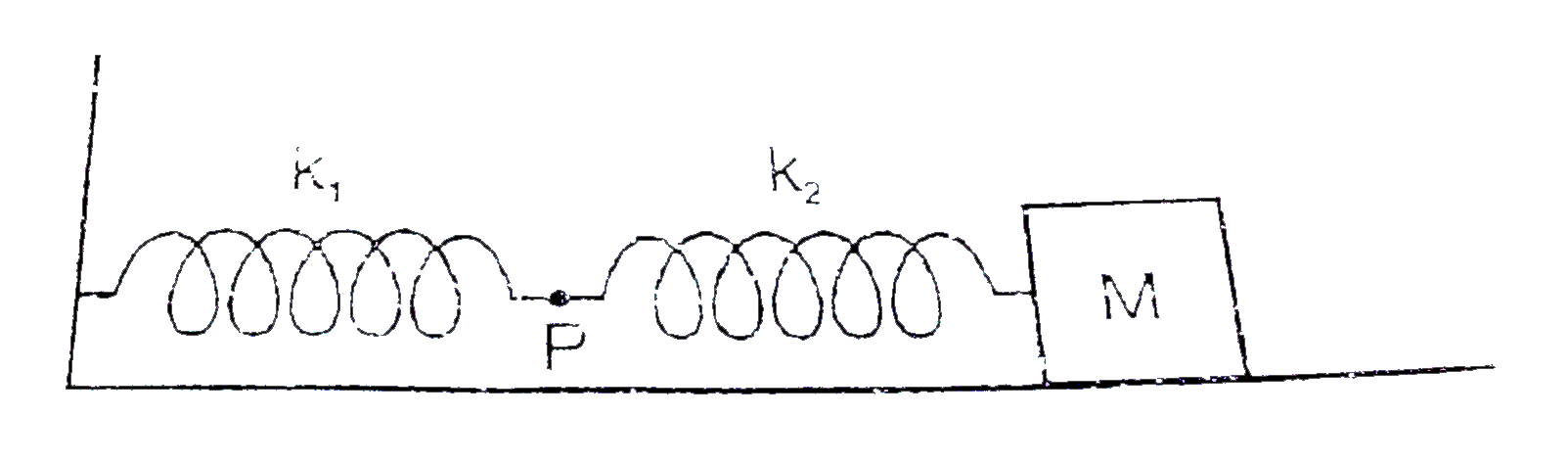Ak1Ak2Bk2Ak1Ck1Ak1+k2Dk2Ak1+k2
A violin string 30.0 cm long with linear density 0.650 g/m is placed near a loudspeaker that is fed by an audio oscillator of variable frequency. It is found that the string is set into oscillation only at the frequencies 1040 and 1560 Hz as the frequency of the oscillator is varied over the range 600-1600 Hz. What is the tension in the string?
View SolutionFind the frequency of small oscillations of thin uniform vertical rod of mass m and length l hinged at the point O.
View SolutionA block of mass ‘m’ rests on a piston executing S.H.M. of period 1sec. The amplitude of oscillations so that the mass is separated from the piston is
View SolutionA mass M=5 kg is attached to a string as shown in the figure and held in position so that the spring remains unstretched. The spring constant is 200Nm−1 . The mass M is then released and begins to undergo small oscillations. The amplitude of oscillation is
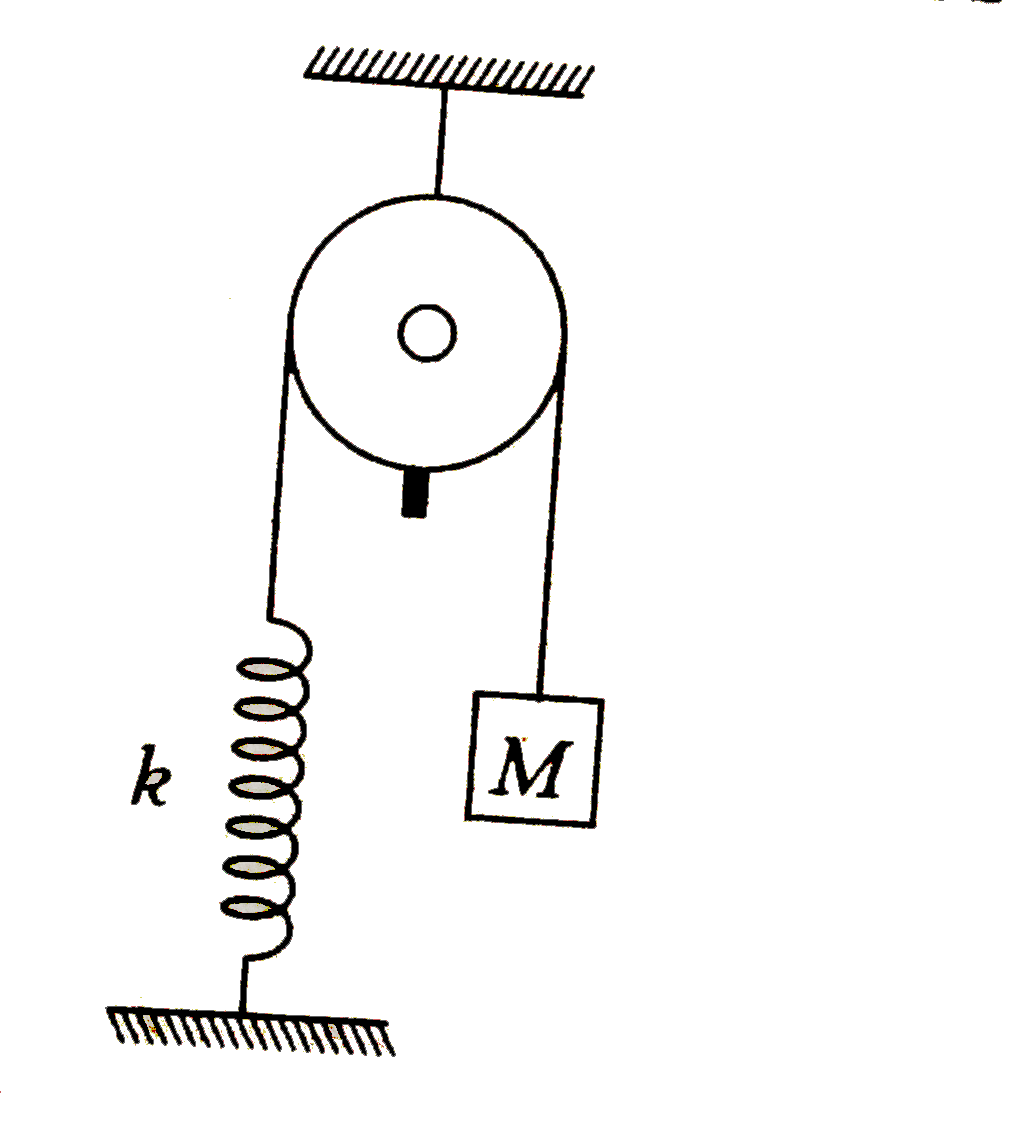
View SolutionThe string of a simple pendulum replaced by a uniform rod of length L and mass M while the bob has a mass m. It is allowed to make small oscillation. Its time period is
View Solution