A sinusoidal wave travels along a string. The time for a particular point to move from maximum placement to zero is 0.135s. What are the (a) period and (b) frequency? (c) The wavelength is 1. 40m, what is the wave speed?
The correct Answer is:(a) 0.540 s (b) 1.85 Hz (c)2.59 m/s
To solve the problem step by step, we will break it down into three parts as per the question.
Step 1: Find the Period (T)
Given that the time for a particular point to move from maximum displacement to zero is 0.135 seconds, we can determine the period of the wave.
1. The motion from maximum displacement to zero represents a quarter of the wave's period (T/4).
2. Therefore, we can express the relationship as:
T4=0.135 seconds
3. To find the full period (T), we multiply both sides by 4:
T=0.135×4=0.54 seconds
Step 2: Find the Frequency (f)
The frequency is the reciprocal of the period.
1. The formula for frequency is:
f=1T
2. Substituting the value of T we found:
f=10.54≈1.85 Hz
Step 3: Find the Wave Speed (v)
We are given the wavelength (λ) as 1.40 m. The wave speed can be calculated using the formula:
v=f×λ
1. Substituting the values we have:
v=1.85 Hz×1.40 m
2. Calculating the wave speed:
v≈2.59 m/s
Final Answers:
(a) The period (T) is 0.54 seconds.
(b) The frequency (f) is approximately 1.85 Hz.
(c) The wave speed (v) is approximately 2.59 m/s.
---
2. Therefore, we can express the relationship as:
T4=0.135 seconds
3. To find the full period (T), we multiply both sides by 4:
T=0.135×4=0.54 seconds
f=1T
2. Substituting the value of T we found:
f=10.54≈1.85 Hz
v=f×λ
v=1.85 Hz×1.40 m
2. Calculating the wave speed:
v≈2.59 m/s
(a) The period (T) is 0.54 seconds.
(b) The frequency (f) is approximately 1.85 Hz.
(c) The wave speed (v) is approximately 2.59 m/s.
Topper's Solved these Questions
- WAVES-IBook:RESNICK AND HALLIDAYChapter:WAVES-IExercise:Practice Questions (Single Correct Choice Type)
Explore 33 Videos
- WAVES-IBook:RESNICK AND HALLIDAYChapter:WAVES-IExercise:Practice Questions (More than One Coorect Choice Type)
Explore 10 Videos
- WAVES-IBook:RESNICK AND HALLIDAYChapter:WAVES-IExercise:Checkpoint
Explore 8 Videos
- WAVE - IIBook:RESNICK AND HALLIDAYChapter:WAVE - IIExercise:PRACTICE QUESTIONS (INTEGER TYPE)
Explore 5 Videos
- WORK, POWER, AND ENERGYBook:RESNICK AND HALLIDAYChapter:WORK, POWER, AND ENERGYExercise:PRACTICE QUESTIONS (Integer Type)
Explore 5 Videos
Similar Questions
A sinusoida wave is travelling along a rope. The oscillator that generates wave completes 40.0 vibration in 30.0 s. also, a given 'maximum' travels 425 cm along the rope in 10.0 s. what is the wavelength of the wave ?
View SolutionA sinusoidal wave travels along a string under tension. Figure 16-52 gives the slopes along the string at time t=0. The scale of the x axis is st by xs=0.40m What is the amplitude of the wave?
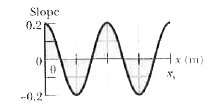
View Solution
Knowledge Check
In a sinusoidal wave, the time required for a particular point to move from maximum displacement to zero displacement is 0.170 second. The frequency of the wave is
A0.73 HzB0.36 HzC1.47 HzD2.94 HzIn a sinusoidal wave, the time required for a particular point to move from maximum displacement to zero displacement is 0.170 second. The frequency of the wave is
A1.47 HzB0.36 HzC0.73 HzD2.94 HzIn a sinusoidal wave, the time required by a particular particle to move from maximum displacement to zero displacement is 0.025 sec. The frequency of the wave is
A2.5 HzB5 HzC7.5 HzD10 Hz
The wave function for a travelling wave on a taut string is
y(x,t)=(0.350m)sin(10πt−3πx+π/4). (SI units)
(a) what is the speed and direction of travel of the wave ?
(b) what if the vertically position of an element of the string at t=0,x=0.100m?
(c ) what is the wavelength and frequency of the wave?
(d) what is the maximum transverse speed of an element of the string?
View SolutionA sinusoidal wave is propagating along a streched string that lies along the x-axis. The displacement of the string as a function of time is graphed in for particles at x-0 and at x=0.0900 m. (a) what is the amplitude of the wave? (b)what is the period of the wave? (c ) you are told that the two points x=0 and x=0.0900 m are within one wavelength of each other. if the wave is moving in the +x-direction, determine the wavelength and the wave speed. (d) if instead the wave is moving in the -x-direction, determine the wavelength and the wave speed. (e) would it be possible to derermine definitely the wavelength in parts (c ) and (d) if you were not told that the two points were within one wavelength of each other? why ot why not?
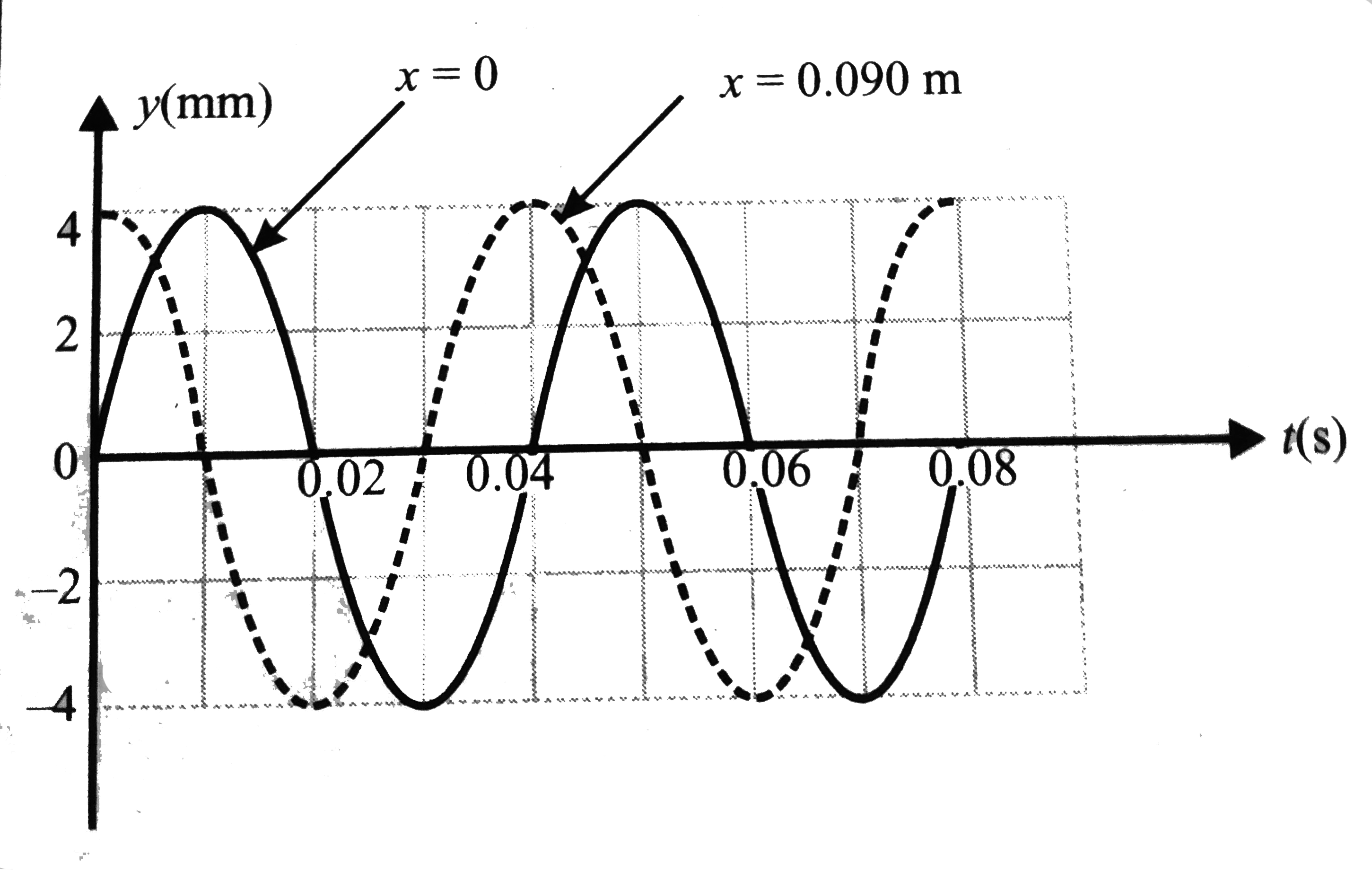
View SolutionA sinusoidal wave propagates along a string. In figure (a) and (b)'y' represents displacement of aprticle from the mean position. 'x'&'t' have usual meanings . Find :
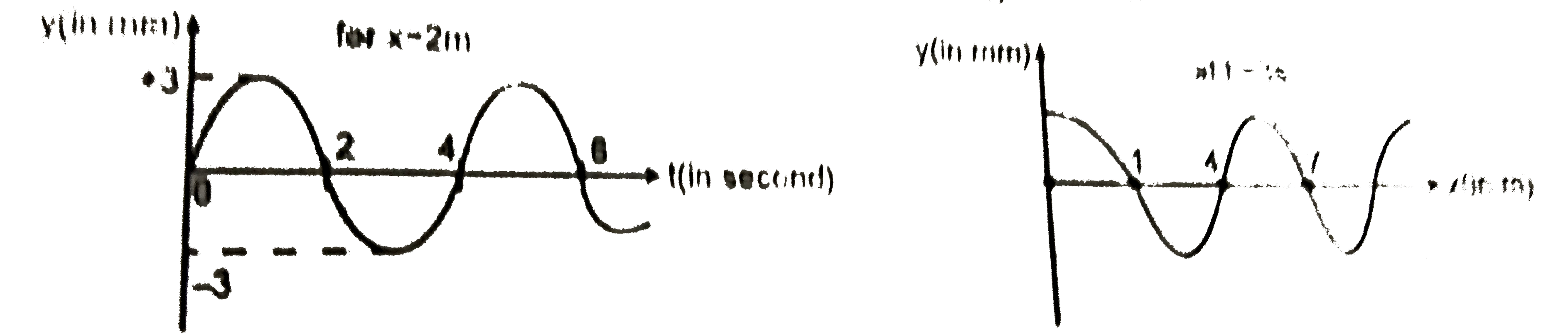
(a) wavelength, freuency and speed of the wave.
(b) maximum velocity and maximum acceleration of the particles.
(c) the magnitude of slopes of the string at x=2 at t=4sec.
View SolutionIn a sinusoidal wave the time required for a particular point to moce from equilibrium pasition to maximum diaplacement is 0.17s, then the frequency of wave is:
View SolutionA sound wave travels at a speed of 340ms−1 . If its wavelength is 2 cm, what is the frequency of the wave ?
View Solution

