A sinusoidal wave is propagating along a streched string that lies along the x-axis. The displacement of the string as a function of time is graphed in for particles at x-0 and at x=0.0900 m. (a) what is the amplitude of the wave? (b)what is the period of the wave? (c ) you are told that the two points x=0 and x=0.0900 m are within one wavelength of each other. if the wave is moving in the +x-direction, determine the wavelength and the wave speed. (d) if instead the wave is moving in the -x-direction, determine the wavelength and the wave speed. (e) would it be possible to derermine definitely the wavelength in parts (c ) and (d) if you were not told that the two points were within one wavelength of each other? why ot why not? 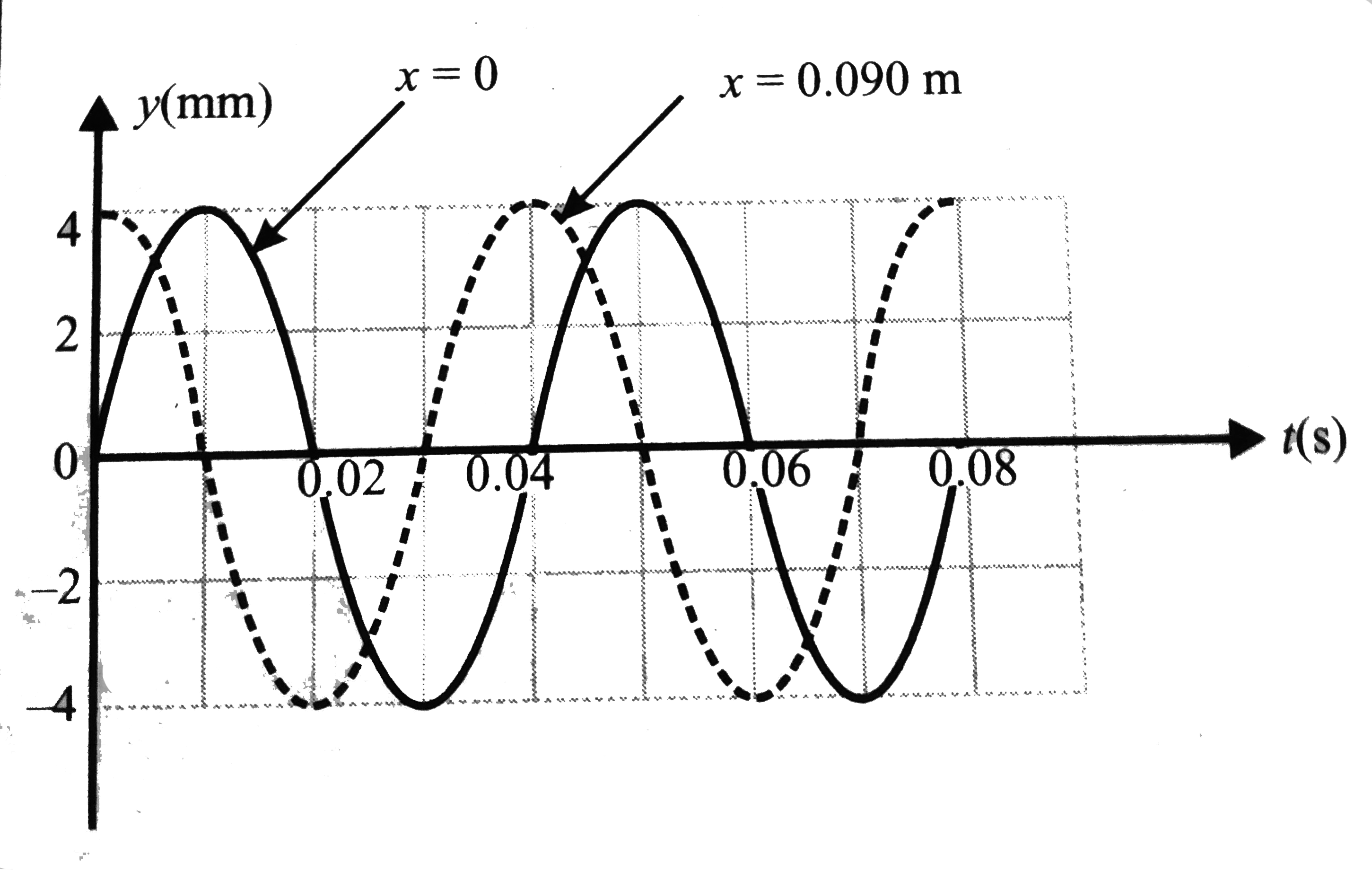
Let equation of wave is y=Asin(ωt−kx+θ)
Vp=dydt=Aωcos(ωt−kx+θ)
atx=0,t=0,we have y=0,vp>0
⇒0=Asinθ⇒θ=0 or π
But vp>0,so θ=0
at t=0,x=0.090m
y=A=4mm→amplitude
A=Asin(−k(0.090))
⇒−k(0.090)=2nπ+π2
⇒−2πλ(0.090)=2nπ+π2
⇒λ=−0.364n+1
for n=−1,λ=0.12m
from graph, time period =T=0.04s
wave speed: v=λT=0.120.04=3m/s
if wave is moving in negativex-direction: let wave equation is
y=Asin(ωt+kx+θ)
Processing as above, we will get λ=0.364n+1
forn=0,lambda=0.36 m<br>wavespeed:v=(lambda)/(T)=(0.36)/(0.04)=9 m//s
Topper's Solved these Questions
- TRAVELLING WAVESBOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Subjective
16 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Single Correct
62 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Exercise 5.1
9 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICSCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct
9 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
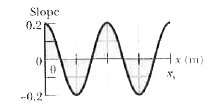
A sinusoidal wave travels along a string under tension. Figure 16-52 gives the slopes along the string at time t=0. The scale of the x axis is st by xs=0.40m What is the amplitude of the wave?
View SolutionA sinusoidal harmonic wave is propagating along a string stretched along x – axis. A particle on the string at x = 1 m is found to be at its mean position travelling in positive y direction at t=1s. The amplitude, wavelength and frequency of the wave are 0.01m,π2m and 20Hz respectively. Write the equation of the wave if-
(a) it is travelling along negative X direction
(b) it is travelling along positive X direction.
View Solution
Knowledge Check
A transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.

Q. The velocity of propagation of the wave is ?A2cm/sB4cm/sC1cm/sD8cm/sA transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.
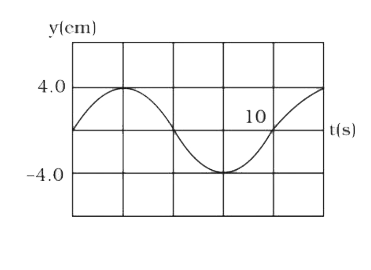
Q. Skecth of one wavelength of the wave (the portion between x=0 and x=20cm) at time t=0 is:A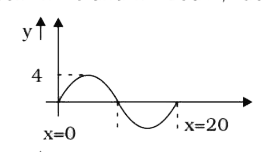 B
B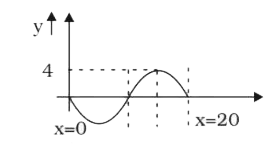 C
C D
D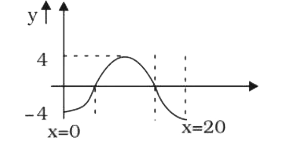
A transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. The transverse displacement of the string particle at as a function of time is shown in Figure.
The equation of the wave with all the constants evaluated is:
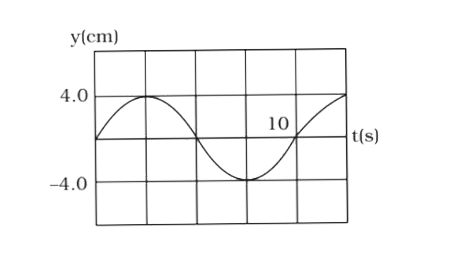 Ay=(4.0cm)sin(π10x−π5t),x in cm and t in sec.By=(4.0cm)sin(π10x+π5t),x in cm and t in secCy=(4.0cm)sin(π10x−π5t+π), x in cm and t in secDy=(4.0cm)cos(π10x−π5t+π),x in cm and t in sec
Ay=(4.0cm)sin(π10x−π5t),x in cm and t in sec.By=(4.0cm)sin(π10x+π5t),x in cm and t in secCy=(4.0cm)sin(π10x−π5t+π), x in cm and t in secDy=(4.0cm)cos(π10x−π5t+π),x in cm and t in sec
A simple harmonic plane wave propagatees along x-axis in a medium. The displacement of the particle as a function of time is shown in figure, for x=0(curve 1) and x=7 (curve 2)
The two particle are with a span of onewavelength.
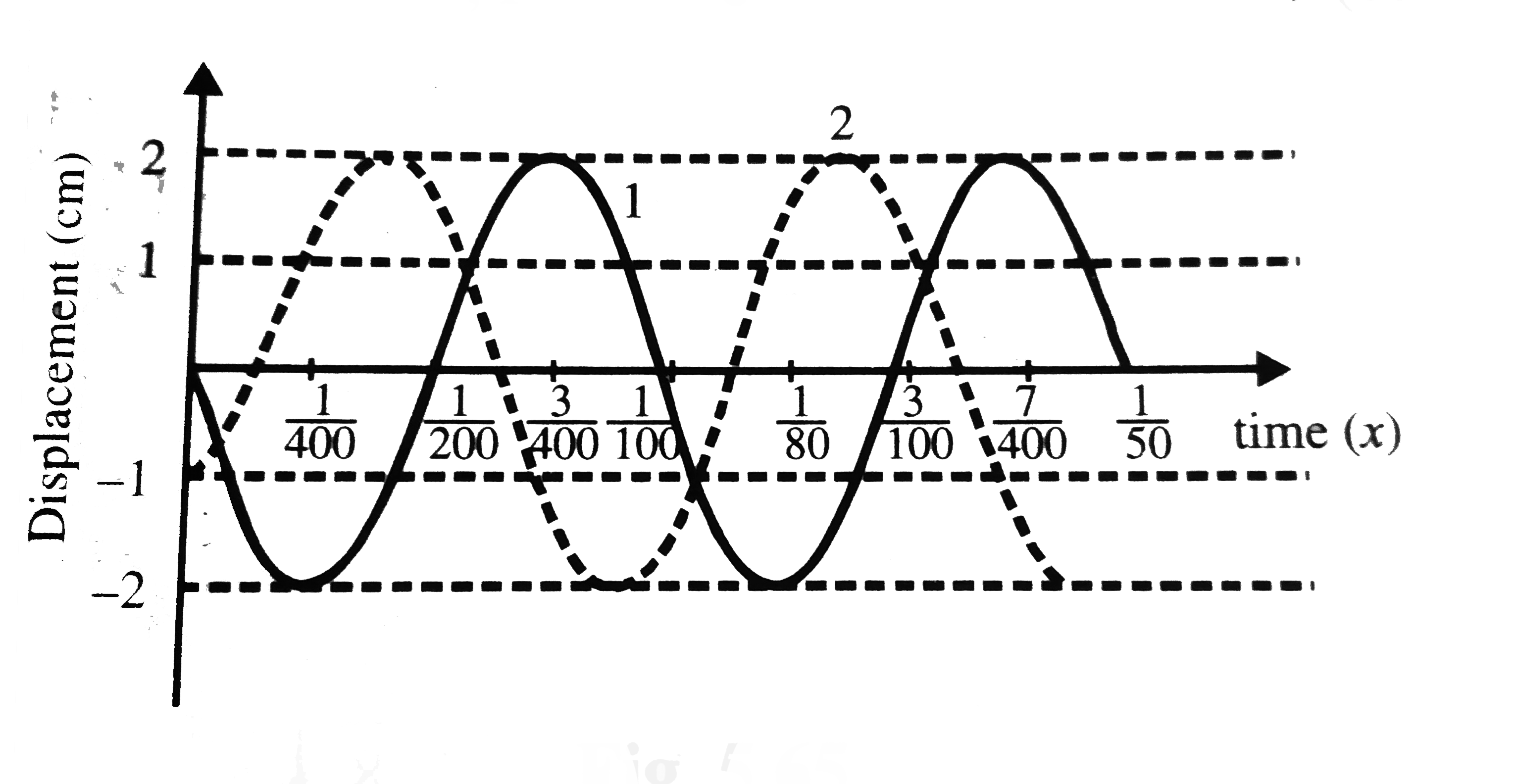
The wavelength of the wave is
View SolutionA transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.
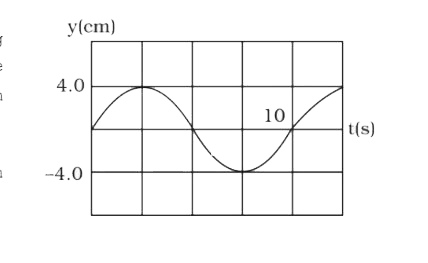
Q. The transverse velocity of the particle at x=0 at t=5.0 s is ?
View SolutionA harmonic wave is travelling along +ve x-axis, on a stretched string. If wavelength of the wave gets doubled, then
View SolutionA wave along a string has the equation y=0.02sin(30t−4x), where x and y are in m and t in second the amplitude of the wave is
View SolutionA sinusoidal wave is propagating in negative x-direction in a string stretched along x-axis. A particle of string at x=2 cm is found at its mean position and it is moving in positive y-direction at t=1 s. the amplitude of the wave, the wavelength and the angular frequency of the wave are 0.1m,π/4m and 4πrad/s, respectively.
The equation of the wave is
View Solution
