A wave is propagating along the length of a string taken as positive x-axis. The wave equation is given by
y=Ae(−tt−xA)2
where A=5mm, T=1.0 s and λ=8.0cm
(a) Find the velocity of the wave. (b) find the function f(t) represent the displacement of particle at x=0. (c ) Plot the function g(x) representing the shape of the string at t=0 (d) Plot the function g(x) of the string at t=0 and t=5 s
(a). The wave equation is
y=Ae−(tT−xλ)2
This may be expressed as
y=Ae−1λ2(x−λT1)2
This is the form f(x−vt)
Therefore,the velocity of wave v=λ/T=8.0/1.0=8cm/s
(b). substituting t=0 in given Eq. (i),we get
f(t)=Ae−(t/T)2
(c ) substituting t=0 in given Eq.(i), we get
g(x)=aE(−(X/LAMBDA)2)
(d). At t=0, the displacement is maximum at the originwhile at t=5s, the displacement is maximum at distance x=vt=8×5=40cm
The function g(x) at t=0 and 5s are plotted in s−5.2 (a) and (b)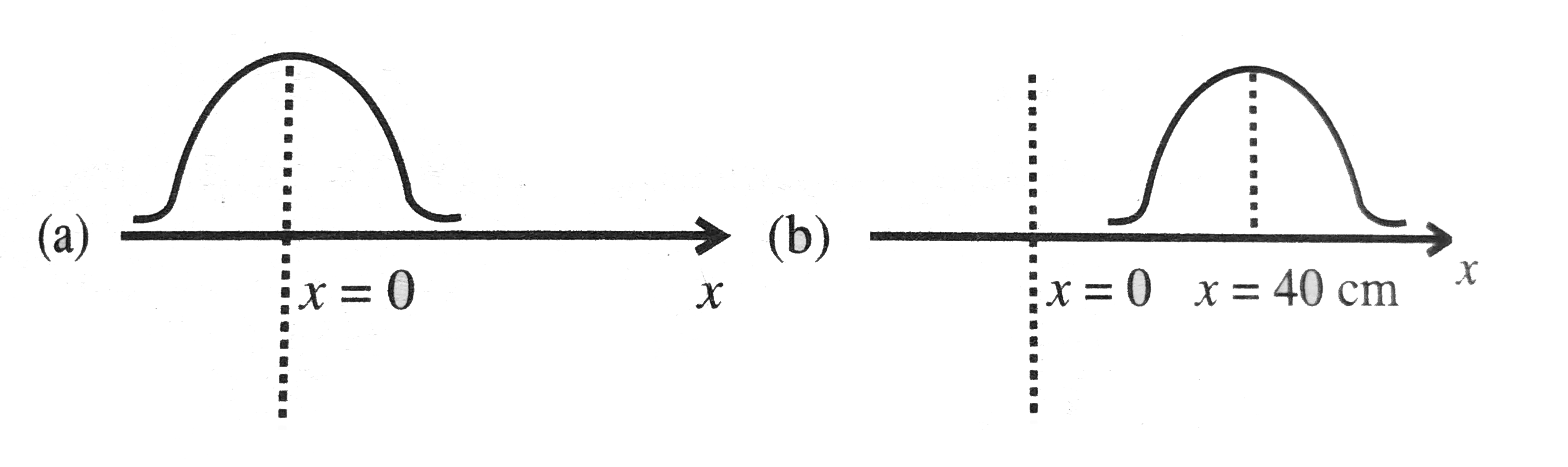
Topper's Solved these Questions
- TRAVELLING WAVESBOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Subjective
16 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Single Correct
62 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Exercise 5.1
9 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICSCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct
9 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A wave is propagating on a long stretched string along its length taken as positive x-axis the wave equation is given by
y=y0e−(tT−xλ)2,wherey0=2mm
T = 1 . 0 sec and λ=6cm find .
Plot the shape of the string at t = 6 sec.
View SolutionA wave is propgting of a long stretched string along its length taken as the positive x-axis. The wave equation is given as
y=y0e−(tT−xλ)^2
where y0=4mm,T=1.0sandλ=4cm. d. Find the velocity of the particle t x=0. c. Find the function g(x) giving the shape of the string t t=0. d. Plot the shape g(x) of the string at t=0. e. Plot of the shape of the string at t=5s.
View Solution
Knowledge Check
The equation of a wave is y=5sin(t0.04−x4) where x is in cm and t is in seccond. The velocity of the wave will be
A1ms−1B2ms−1C1.5ms−1D1.25ms−1The equation of a wave is y=5sin(t0.004−x4) where x is in cm and t is in second the maximum velocity of the wave will be
A1ms−1B2ms−1C1.5ms−1D1.25ms−1The equation of a wave is y=5sin(t0.004−x4) where x is in cm and t is in second the maximum velocity of the wave will be
A1ms−1B2ms−1C1.5ms−1D1.25ms−1
A wave is propagating on a long stretched string along its length taken as positive x-axis the wave equation is given by
y=y0e−(tT−xλ)2,wherey0=2mm
T = 1 . 0 sec and λ=6cm find .
Plot the shape of the string at t = 6 sec.
View SolutionA wave pulse is travelling on a string at 2 m/s. displacement y of the particle at x = 0 at any time t is given by
y=2t2+1
Find
(ii) Shape of the pulse at t = 0 and t = 1s.
View SolutionThe displacement function of a wave traveling along positive x-direction is y=12+2x2 at t=0and by y=12+2(x−2)2 at t=2s, where y and x are in metre. The velocity of the wave is:
View SolutionThe equation of a travelling wave is given by
y = 0.5 sin(20x - 400t)
where x and y are in metre and t is in second. The velocity of the wave is :
View SolutionThe equation of a travelling wave is given by
y = 0.5 sin(20x - 400t)
where x and y are in metre and t is in second. The velocity of the wave is :
View Solution
