In Fig. a "semi-infinite" nonconducting rod (that is, infinite in one direction only) has uniform linear charge density λ. (a) show that the electric field →Epat point P makes an angle 45∘ with the rod and that this result is independent of the distance R. (Hint : Separetly find the component of →Ep parallel to the rod and the component perpendicular to the rod.) (b) Find the the field magnitude for linear charge density 4.52 nC/m and R = 3.80 cm.

(b) 1.51×103N/C
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBook:RESNICK AND HALLIDAYChapter:ELECTRIC CHARGES AND FIELDSExercise:Practice Questions (Single Correct Choice Type)
Explore 45 Videos
- ELECTRIC CHARGES AND FIELDSBook:RESNICK AND HALLIDAYChapter:ELECTRIC CHARGES AND FIELDSExercise:Practice Questions (More than one correct Type )
Explore 3 Videos
- ELECTRIC CHARGES AND FIELDSBook:RESNICK AND HALLIDAYChapter:ELECTRIC CHARGES AND FIELDSExercise:Check points
Explore 9 Videos
- ELASTICITYBook:RESNICK AND HALLIDAYChapter:ELASTICITYExercise:PRACTICE QUESTIONS (Integer Type)
Explore 3 Videos
- ELECTRIC POTENTIALBook:RESNICK AND HALLIDAYChapter:ELECTRIC POTENTIALExercise:(PRACTICE QUESTIONS) Integer Type
Explore 1 Video
Similar Questions
A semi-infinite insulating rod has linear charge density λ. The electric field atthe pointPshown in figure-1.418 is:

View SolutionA rod of length l, has a uniform positive charge per unit length and a total charge Q. calculate the electric field at a point P located along the long axis of the rod and at a distance a from one end

View Solution
Knowledge Check
Consider a finite charged rod. Electric field at point P (shown) makes an angle θ with horizontal dotted line then angle θ is:-
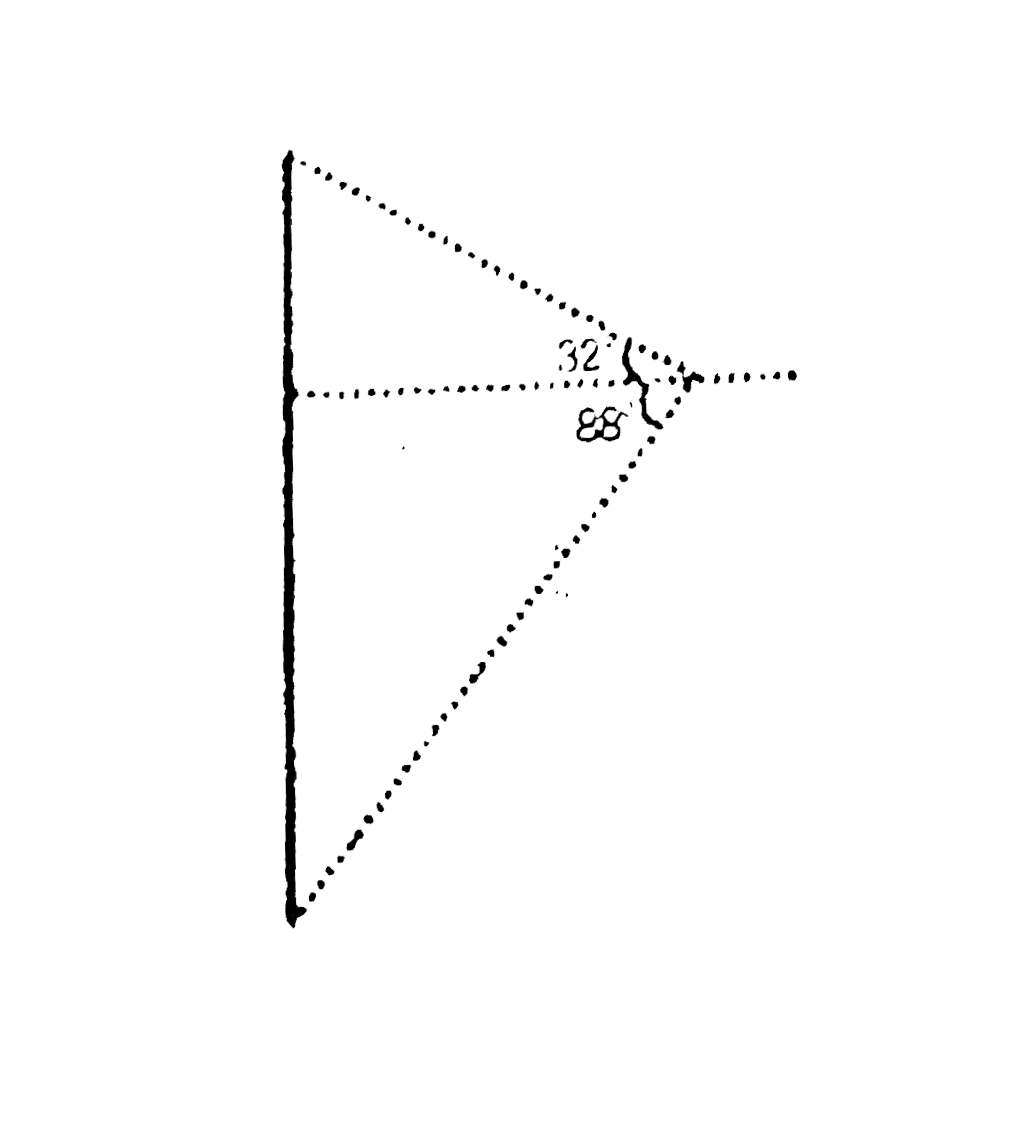 A60∘B28∘C44∘Dinformation insufficient
A60∘B28∘C44∘Dinformation insufficientAn infinitely long wire with linear charge density +λ is bent and the two parts are inclined at angle 30∘ as shown in fig, the electric field at point P is :
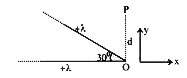 Aλ4π∈0d[(1+√3)ˆi+ˆj]Bλ4π∈0d[(1−√3)ˆi+2ˆj]Cλ4π∈0d[(1+√3)ˆi−2ˆj]Dλ4π∈0d[(1+√3)ˆi+2ˆj]
Aλ4π∈0d[(1+√3)ˆi+ˆj]Bλ4π∈0d[(1−√3)ˆi+2ˆj]Cλ4π∈0d[(1+√3)ˆi−2ˆj]Dλ4π∈0d[(1+√3)ˆi+2ˆj]Find the electric field at point P (as shown in figure) on the perpendicular bisector of a uniformly charged thin wire of length L carrying a charge Q. The distance of the point P from the centre of the rod is a =√32L.
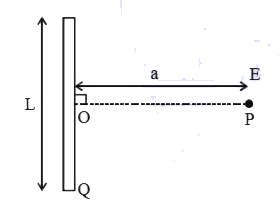 A√3Q4πε0L2BQ3πε0L2CQ2√3πε0L2DQ4πε0L2
A√3Q4πε0L2BQ3πε0L2CQ2√3πε0L2DQ4πε0L2
Consider a finite charged rod. Electric field at point P (shown) makes an angle θ with horizontal dotted line then angle θ is:-

View SolutionA rod of length l, has a uniform positive charge per unit length and a total charge Q. calculate the electric foeld at a point P located along the long axis of the rod and at a distance a from one end

View SolutionAn infinitely long wire with linear charge density +λ is bent and the two parts are inclined at angle 30∘ as shown in fig, the electric field at point P is :

View SolutionIntensity of electric field at a point at a perpendicular distance .r. from an infinite line charge, having linear charge density .λ. is given by :
View SolutionElectric Field||E due to rods
View Solution

