A uniform electric field exists in a region between two oppositely charged plates. An electron is released from rest at the surface of the negatively charged plate and strikes the surface of the opposite plate, 3.0 cm away, in a time 1.5×10−8s. Just as the electron strikes the second plate, what are the its (a) momentum magnitude and (b) kinetic energy ? (c ) What is the magnitude of the electric field →E ?
To solve the problem step by step, we will find the momentum magnitude, kinetic energy, and the magnitude of the electric field.
Given Data:
- Distance between plates, s=3.0cm=3.0×10−2m
- Time taken, t=1.5×10−8s
- Mass of electron, m=9.1×10−31kg
Step 1: Calculate the acceleration of the electron
We can use the second equation of motion:
s=ut+12at2
Since the electron is released from rest, u=0:
s=12at2
Rearranging for a:
a=2st2
Substituting the values:
a=2×(3.0×10−2)(1.5×10−8)2
Calculating t2:
t2=(1.5×10−8)2=2.25×10−16s2
Now substituting this back into the equation for a:
a=2×3.0×10−22.25×10−16=6.0×10−22.25×10−16=2.67×1014m/s2
Step 2: Calculate the final velocity of the electron
Using the first equation of motion:
v=u+at
Since u=0:
v=at=(2.67×1014)×(1.5×10−8)=4.005×106m/s
Step 3: Calculate the momentum magnitude
The momentum p is given by:
p=mv
Substituting the values:
p=(9.1×10−31)×(4.005×106)=3.65×10−24kg m/s
Step 4: Calculate the kinetic energy
The kinetic energy K is given by:
K=12mv2
Substituting the values:
K=12×(9.1×10−31)×(4.005×106)2
Calculating v2:
v2=(4.005×106)2=1.604×1013m2/s2
Now substituting back:
K=12×(9.1×10−31)×(1.604×1013)=7.29×10−18J
Step 5: Calculate the magnitude of the electric field
The force F on the electron is given by:
F=ma
Using F=qE where q=−1.6×10−19C:
ma=qE⟹E=maq
Substituting the values:
E=(9.1×10−31)×(2.67×1014)1.6×10−19
Calculating:
E=2.43×10−161.6×10−19=1.52×103N/C
Final Answers:
(a) Momentum magnitude: 3.65×10−24kg m/s
(b) Kinetic energy: 7.29×10−18J
(c) Magnitude of the electric field: 1.52×103N/C
- Distance between plates, s=3.0cm=3.0×10−2m
- Time taken, t=1.5×10−8s
- Mass of electron, m=9.1×10−31kg
We can use the second equation of motion:
s=ut+12at2
Since the electron is released from rest, u=0:
s=12at2
Rearranging for a:
a=2st2
Substituting the values:
a=2×(3.0×10−2)(1.5×10−8)2
Calculating t2:
t2=(1.5×10−8)2=2.25×10−16s2
Now substituting this back into the equation for a:
a=2×3.0×10−22.25×10−16=6.0×10−22.25×10−16=2.67×1014m/s2
Using the first equation of motion:
v=u+at
Since u=0:
v=at=(2.67×1014)×(1.5×10−8)=4.005×106m/s
The momentum p is given by:
p=mv
Substituting the values:
p=(9.1×10−31)×(4.005×106)=3.65×10−24kg m/s
The kinetic energy K is given by:
K=12mv2
Substituting the values:
K=12×(9.1×10−31)×(4.005×106)2
Calculating v2:
v2=(4.005×106)2=1.604×1013m2/s2
Now substituting back:
K=12×(9.1×10−31)×(1.604×1013)=7.29×10−18J
The force F on the electron is given by:
F=ma
Using F=qE where q=−1.6×10−19C:
ma=qE⟹E=maq
Substituting the values:
E=(9.1×10−31)×(2.67×1014)1.6×10−19
Calculating:
E=2.43×10−161.6×10−19=1.52×103N/C
(a) Momentum magnitude: 3.65×10−24kg m/s
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (Single Correct Choice Type)
45 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (More than one correct Type )
3 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Check points
9 Videos
- ELASTICITYBOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type
1 Videos
Similar Questions
A uniform electric field exists in the region between toe oppositely charged plane parallel plates. An electron is released from rest at the surface of the negatively charged plate and strikes the surface of the opposition plate 2 cm away from the first in an intercval of 1.5×10−8s . Find (a) the electric intensity ,(b) the velocity of the electron when it strikes the second plate.
View SolutionA uniform electric field E exists between two oppositely charged plates (Fig. 3.38). What will be the work done in moving a charge q along a closed rectangular path ?
 .
.
View Solution
Knowledge Check
A uniform electric field →E exists between the plates of a charged condenser. A charged particle enters the space between the plates and perpendiculars to →E. The path of the particle between the plates is a
AStraight lineBhyperbolaCparabolaDcircleWhen 1020 electrons are removed from the surface of a neutral metal plate, the electric charge on it (in coulomb) is
A+16B−1.6C10−19D1019The surface charge densities on two square plates of a parallel plate capacitor are to +σand−σ respectively. What is the magnitude of the electric field in the region between the plates?
Aσ2ε0Bσε0C0DNone of these
The ratio of charge on left surface of plate A to the charge on the right surface of plate B is +Q +3Q -20 (A) (B) (C)
View SolutionThe distance between charged parallel plates is d. An electron -proton is released somewhere in the gap between the plates and it is found that the proton reaches the negative plate at the same time as electron reaches the positive plate. At consider only electric force. The mass of electron is me and mass of proton is mp.The electric field between plates is E.
View SolutionAn electron is projected as in figure with kinetic energy K, at an angle θ=45∘ between two charged plates. The magnitude of the electric field so that the electron just fails to strike the upper plate, should be greater than:
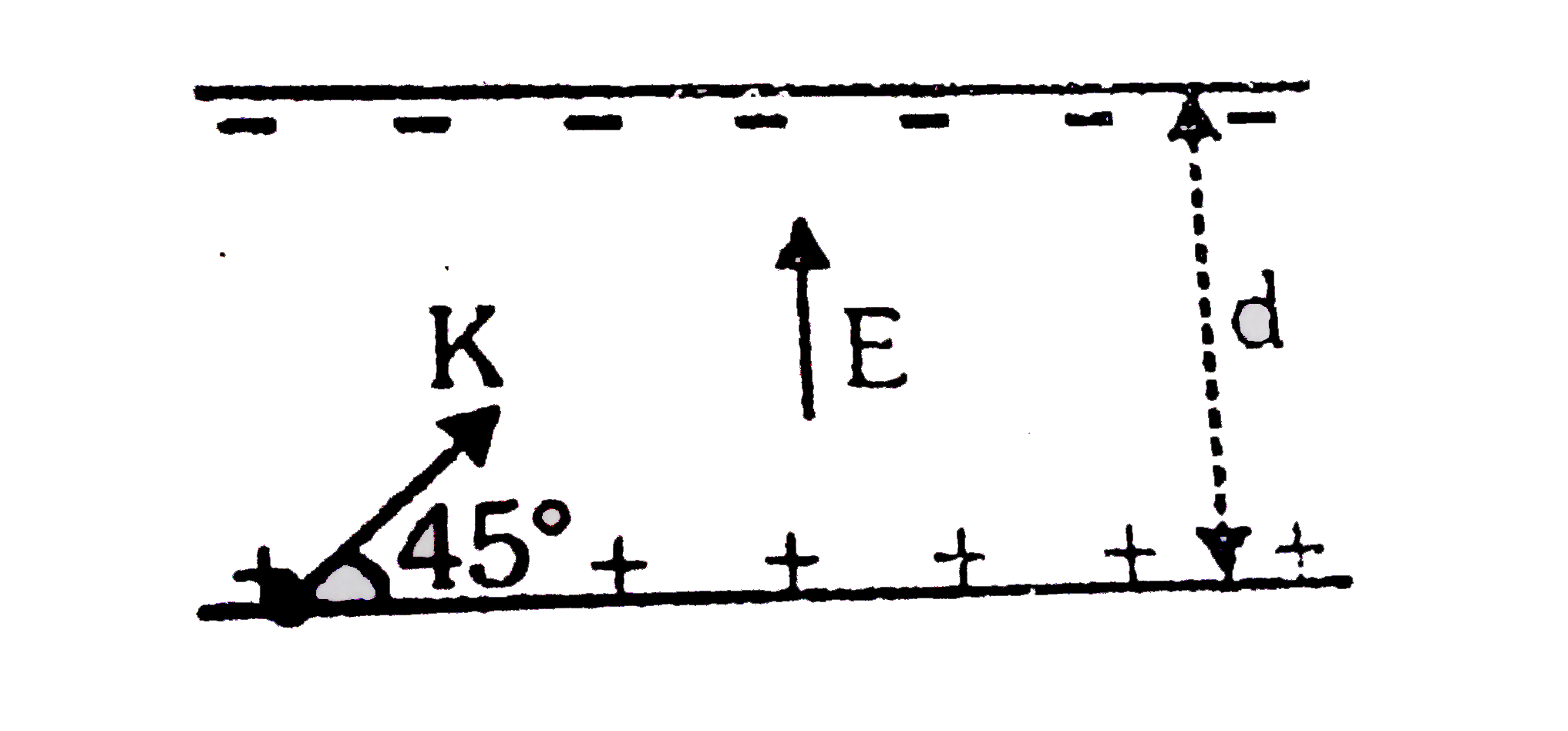
View SolutionAn electron is projected as shown in fig. with kinetic energy K, at an angle θ=45∘ between two charged plates. Ignore the gravity.
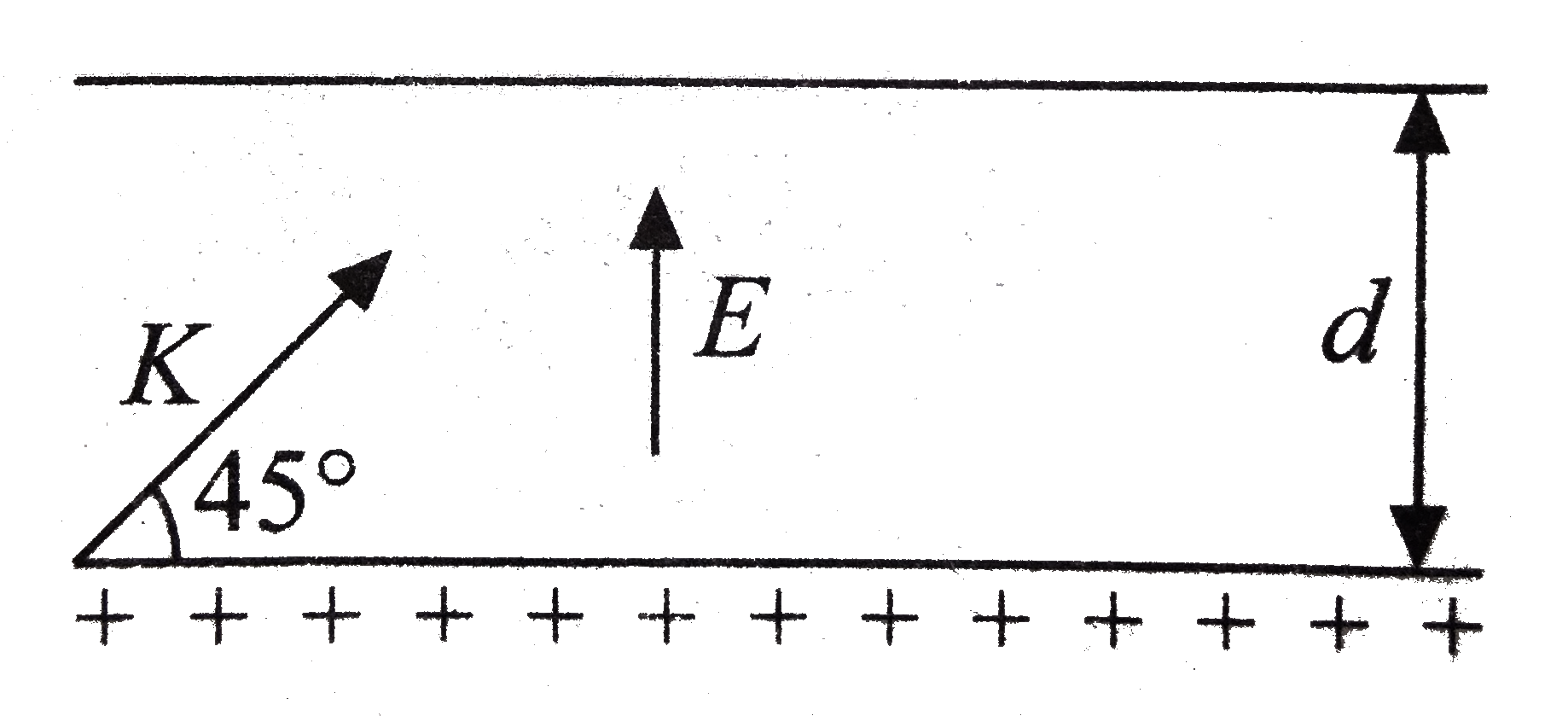
At what distance from the starting point will the electron strike the lower plate?
View Solutionv33.2
View Solution
