A rod of length l, has a uniform positive charge per unit length and a total charge Q. calculate the electric field at a point P located along the long axis of the rod and at a distance a from one end

The field d→E at P due to each segment of charge on the rod is in the negative x direction because every segment carries a positive charge.
Because the rod is continous we are evaluating the field due to a continuous charge distribution rather than a group of individual charges. Because every segment of the negative x direction, the sum of their contributions can be handled without the need to add vectors.
Let us assume the rod is lying along the x-axis , dx is the length of one small segment and dq is the charge on that segment. Beacuse the rod has a charge per unt length 1, the charge dq on the small segment is dq=λdx. The magnitude of the electric field at P due to one segment of the rod having a charge dq is
dE=kedqx2=keλdxx2
The total field at P is
E=∫l+aaKeλdxx2
If Ke and λ=Q/l are constants and can be removed from the integral, them
E=∫l+aakeλdxx2[−1x]l+aa
=keQl(1a−1l+a)=keQa(l+a)
If a to b, which corresponds to sliding the bar to the left until its left end is at the origin, then E→∞ that represents the condition in wich the observation point P is at zero distance from the charge at the end of the rod, so the field become infinite.
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Solved examples
Explore 10 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Exercises
Explore 58 Videos
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICS ENGLISHChapter:CENGAGE PHYSICS DPPExercise:subjective type
Explore 51 Videos
- ELECTRIC CURRENT & CIRCUITSBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC CURRENT & CIRCUITSExercise:Kirchhoff s law and simple circuits
Explore 15 Videos
Similar Questions
A ring of radius a contains a charge q distributed. uniformly ober its length. Find the electric field at a point. on the axis of the ring at a distance x from the centre.
View SolutionA rod length l is uniformly charged with charge q. Calculate potential at point P.

View SolutionA very long straight uniformly charged thread carries a charge λ per unit length, Find the magnitude and direction of the electric field strenght at a point which is at a distance y from the thread and lies on the perpendicular passing through one of the thread.s ends.
View SolutionA 10 cm long rod carries a charge of +150μC distributed uniformly along its length. Find the magnitude of the electric field at a point 10 cm from both the ends of the rod.
View SolutionA thin straight rod of length l carrying a uniformly distributed charge q is located in vacuum. Find the magnitude of the electric force on a point charge 'Q' kept as shown in the figure.

View SolutionFind the electric field caused by a disc of radius a with a uniform surfce charge density σ (charge per unit area) at a point along the axis of the disc a distance x from its centre.
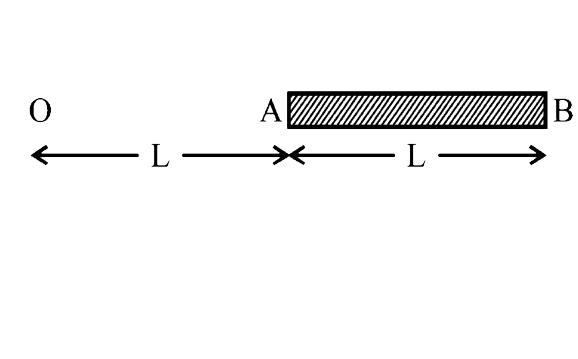
View SolutionA charge Q is uniformly distributed over a long rod AB of length L as shown in the figure. The electric potential at the point O lying at distance L from the end A is
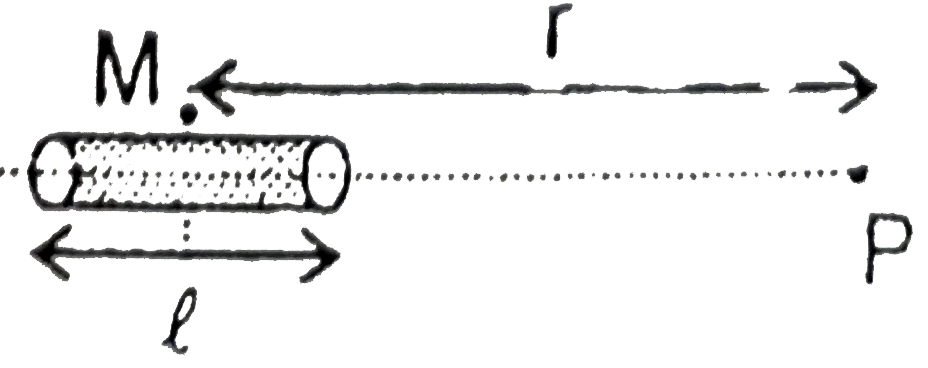
View SolutionA insulating cylindrical rod of diameter d and length l(l>>d) has a uniform surface charge density such that the electric field just outside the curved surface of the cylinder at point M is E0. Find the electric field due to charge distribuition at point P(r>>l).
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA rod of length L has a total charge Q distributed uniformly along its length. It is bent in the shape of a semicircle. Find the magnitude of the electric field at the centre of curvature of the semicircle.
View Solution