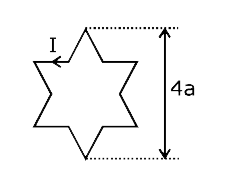
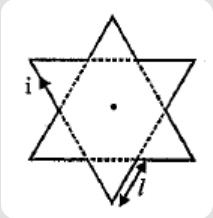
A symmetric star shaped conducting wire loop is carrying a steady state current I as shown in the figure. The distance between the diametrically opposite vertices of the star is 4a. The magnitude of the magnetic field at the center of the loop is
μ0I4πa3[2−√3]
μ0I4πa6[√3−1]
μ0I4πa3[√3−I]
μ0I4πa6[√3+1]
The correct Answer is:B
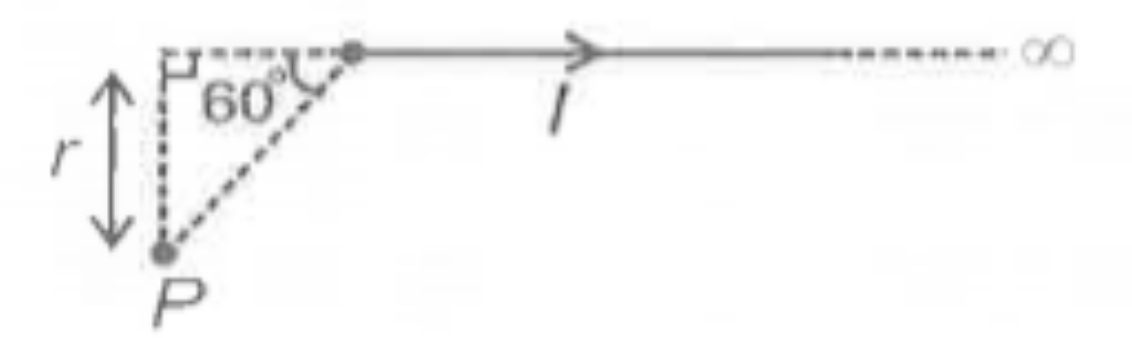
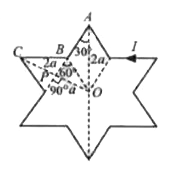
Let us first calculate the magnetic field due to element AB. Perpendicular distance of centre O from element AB, OP= a
Angle subtended by centre at element are θ1=30∘,θ2=60∘ as shown in figure.
∴→B=μ0I4πa(cos30∘−cos60∘)⊙
=μ0I4πa(√32−12)⊙=μ0I8πa(√3−1)⊙
Since the direction of magnetic field due to each element side is out of the paper.
∴ Net magnetic field at O=12×μ0I8πa(√3−1)
=μ0I4πa6(√3−1)
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENTBook:MTG-WBJEEChapter:MAGNETIC EFFECT OF CURRENTExercise:WB JEE Previous Years Questions
Explore 22 Videos
- LAWS OF MOTION Book:MTG-WBJEEChapter:LAWS OF MOTION Exercise:WB JEE PREVIOUS YEARS QUESTIONS (CATEGORY 3: ONE OR MORE THAN ONE OPTION CORRECT TYPE (2 MARKS))
Explore 2 Videos
- MAGNETICSBook:MTG-WBJEEChapter:MAGNETICSExercise:WB JEE Previous Years Questions (Category 3: One or More than one Option)
Explore 2 Videos
Similar Questions
Knowledge Check
A square loop of side a carries a current I. The magnetic field at the center of the loop is
A2μ0I√2πaBμ0I√2πaC4μ0I√2πaDμ0IπaA wire bent in the shape of a regular n-polygonal loop carries a steady current I. Let l be the perpendicular distance of a given segment and R be the distance of vertex both from the centre of the loop. The magnitude of the magnetic field at the centre of the loop is given by -
Anμ0I2πlsin(π/n)Bnμ0I2πRsin(π/n)Cnμ0I2πlcos(π/n)Dnμ0I2πRcos(π/n)A square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
Aindependent of LBproportional LCinversely proportional to LDlinearly proportional to L
A square loop is carrying a steady current I and the magnitude of its magnetic dipole moment is m.If this square loop is changed to a circular loop and it carries the same current the magnitude of the magnetic dipole moment of circular loop will be
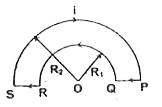
View SolutionThe wire loop shown in figure carries a current as shown. The magnetic field at the centre O is ,
View SolutionA rectangular loop of metallic wire is of length a and breadth b and carries a current i. The magnetic field at the centre of the loop is
View SolutionAn equilateral triangular loop of wire of side / carries a current I. The magnetic field produced at the circumcentre of the loop is
View SolutionA star shaped loop ( with l= length of each section ) carries current i. Magnetic field at the centroid of the loop is
View Solution