A solution curve of the differential equation $(x^{2} + x y + 4 x + 2 y + 4) (\frac{d y}{d x}) - y^{2} = 0$ passes through the point $(1, 3)$ Then the solution curve is

A

intersects y = x + 2 exactly at one point

B

intersects y = x + 2 exactly at the two points

C

intersects y = ${(x + 2)}^{2}$

D

does not intersect $y = {(x + 3)}^{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, D

Given, $(x^{2} + x y + 4 x + 2 y + 4) \frac{d y}{d x} - y^{2} = 0$
$\Rightarrow [(x^{2} + 4 x + 4) + y (x + 2)] \frac{d y}{d x} - y^{2} = 0$
$\Rightarrow [{(x + 2)}^{2} + y (x + 2)] \frac{d y}{d x} - y^{2} = 0$
Put x + 2 = X and y = Y, then
$(X^{2} + X Y) \frac{d Y}{d X} - Y^{2} = 0$
$\Rightarrow$ X(2) dY + XYdY - Y^(2) dX = 0 $< b r >$ implies $X^{2} d Y + Y (X d Y - Y d X) = 0$
$\Rightarrow - \frac{d Y}{Y} = \frac{X d Y - Y d X}{X^{2}}$
$\Rightarrow - d (log | Y |) = d (\frac{Y}{X})$
On integrating both sides, we get
$- log | Y | = \frac{Y}{X} + C$ , where $x + 2 = X$
and $y = Y$
$\Rightarrow - log | y | = (y) = \frac{y}{x + 2} + C$
Since, it passes through the point (1,3)
$∴ - log 3 = 1 + C$
$\Rightarrow C = - 1 - log 3 = - (log e + log 3) = - log 3 e$
$∴$ Eq (i) becomes
$log | y | + \frac{y}{x + 2} - log (3 e) = 0$
$\Rightarrow log (\frac{| y |}{3 e}) + \frac{Y}{x + 2} = 0$
Now, to check option (a), y = x + 2 intersects the curve.
$\Rightarrow log (\frac{| x + 2 |}{3 e}) + \frac{x + 2}{x + 2} = 0$
$\Rightarrow log (\frac{| x + 2 |}{3 e}) = - 1$
$\Rightarrow \frac{| x + 2 |}{3 e} = e^{- 1} = \frac{1}{e}$
$\Rightarrow | x + 2 | = 3$ or $x + 2 = \pm 3$
$∴ x = 1$ , -5 (rejected) =, as $x > 0$
$∴ x = 1$ only one solution.
Thus, (a) is the correct answer.
To check option (c ), we have
$y = {(x + 2)}^{2}$ and $log . (\frac{| y |}{3 e}) + \frac{y}{x + 2} = 0$
$\Rightarrow log [\frac{{| x + 2 |}^{2}}{3 e}] + \frac{{(x + 2)}^{2}}{x + 2} = 0$
$\Rightarrow log [\frac{{| x_{2} |}_{2}^{2}}{3 e}] = - (x + 2)$
$\Rightarrow \frac{(x + 2^{2})}{3 e} = e^{- (x + 2)}$ or ${(x + 2)}^{2} e^{x + 2} = 3 e$
$\Rightarrow e^{x + 2} = \frac{3 e}{{(x + 2)}^{3}}$

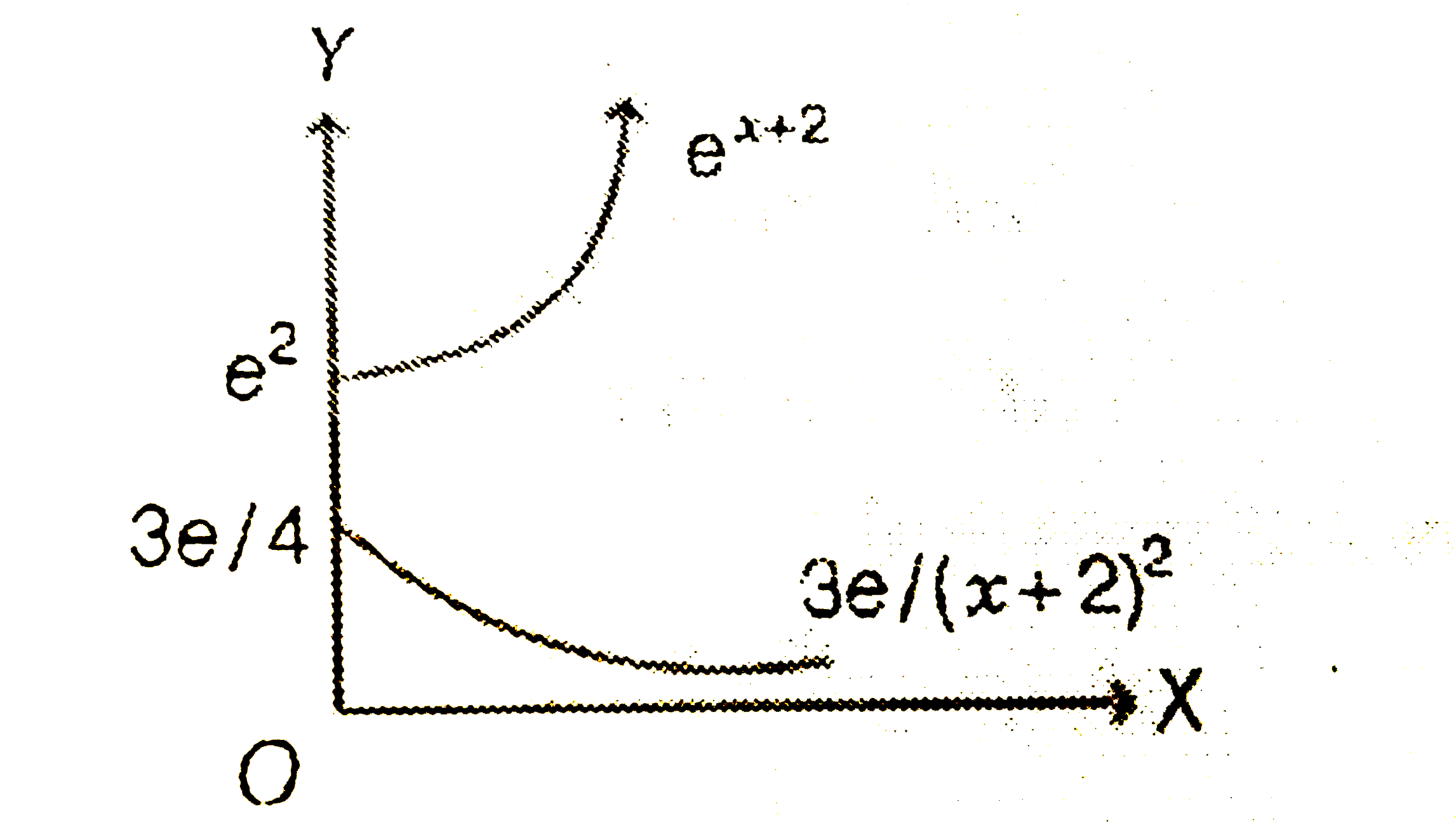
Clearly, they have no solution.
To check option (d), $y = {(x + 3)}^{2}$
i.e., $log [\frac{{| x + 3 |}^{2}}{3 e}] + \frac{{(x + 3)}^{2}}{(x + 2)} = 0$
To check the number of solutions.
Let $g (x) = 2 log (x + 3) + \frac{{(x + 3)}^{2}}{(x + 2)} - log (3 e)$ ltbr $∴ g' (x) = \frac{2}{x + 3} + (\frac{(x + 2) . 2 (x + 3) - {(x + 3)}^{2} .1}{{(x + 2)}^{2}} - 0$
$= \frac{2}{x + 3} + \frac{(x + 3) (x + 1)}{{(x + 2)}^{2}}$
Clearly, when $x > 0$ , then $g' (x) > 0$
$∴$ g (x) in increasing, when $x > 0$
Thus, when $x > 0$ , then g (x) $>$ g (0)
$g (x) > log (\frac{3}{e}) + \frac{9}{4} > 0$
Hence, there is no solution
Thus, option (d) is true.

|

Updated on:21/07/2023

Class 12 MATHS PARABOLA

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The solution curve of the differential equation, $(1 + e^{- x}) (1 + y^{2}) \frac{d y}{d x} = y^{2}$ , which passes through the point (0,1), is:
A $y^{2} = 1 + y {log}_{e} (\frac{1 + e^{- x}}{2})$
B $y^{2} + 1 = y ({log}_{e} (\frac{1 + e^{- x}}{2}) + 2)$
C $y^{2} + 1 = y ({log}_{e} (\frac{1 + e^{x}}{2}) + 2)$
D $y^{2} = 1 + y ({log}_{e} (\frac{1 + e^{x}}{2}))$
Question 2 - Select One
The solution of the differential equation $(2 x - 4 y + 3) \frac{d y}{d x} + (x - 2 y + 1) = 0$ is
Alog [ (2x - 4y)+3] = x - 2y+c
Blog [2(2x-4y)+3]=2(x-2y)+c
Clog[2(x-2y)+5]=2(x+y)+c
Dlog[4(x-2y)+5]=4(x+2y)+c
Question 3 - Select One
Solution of the differential equation $x^{2} \frac{d y}{d x} - 3 x y - 2 y^{2} = 0$ is
Ay=cx(x-y)
By=cx(x+y)
C $y = c x^{2} (x - y)$
D $y = c x^{2} (x + y)$

IIT JEE PREVIOUS YEAR-PARABOLA-TOPIC 3 EQUATION OF NORMAL AND PROPERTIES OBJECTIVES QUESTIONS II (ONE OR MORE THAN ONE CORRECT OPTION )

Home
Ask Doubt
Profile