·If the normals of the parabola y2=4x drawn at the end points of its latus rectum are tangents to the circle (x−3)2(y+2)2=r2 , then the value of r2 is

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:2

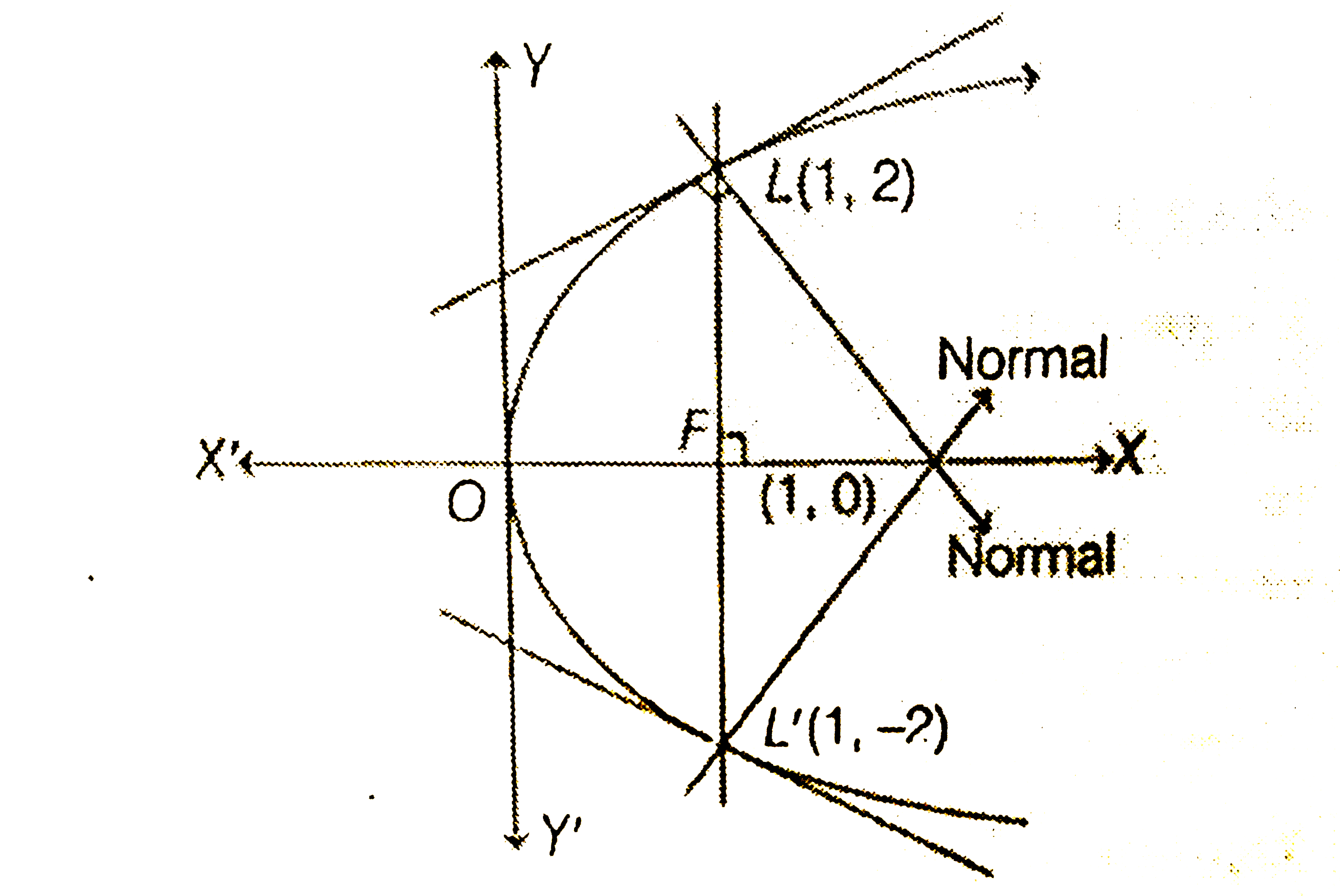
End points of latusrectum are (a±2a) i.e. (1±2)
Equation of normal at (x1,y1) is
y−y1x−x1=y12a
i.e., y−2x−1=−22 and y+2x−1=23
⇒x+y+3
and x−y=3
Which is tangent to (X−3)2+(y+2)2=r2
ocr_image
∴ Length of perpendicular from centre = Radius
⇒|3−2−3|√12+12=r
∴r2=2

Updated on:21/07/2023
|
Class 12MATHSPARABOLA

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The equation of tangents to the parabola y2=4ax at the ends of latus rectum is :

    Ax−y+a=0
    Bx+y+a=0
    Cx+y−a=0
    Dboth (a) and (b)

  • The end points of the latus rectum of the parabola x2+5y=0 is

    A(±52,−54)
    B(±25,±45)
    C(±45,±45)
    D(±54,−52)

  • The end points of latus rectum of the parabola x2=4ay are

    A(a,2a),(2a,a)
    B(−a,2a),(2a,a)
    C(a,−2a),(2a,a)
    D(−2a,a).(2a,a)