Let P be the point on parabola y2=4x which is at the shortest distance from the center S of the circle x2+y2−4x−16y+64=0 let Q be the point on the circle dividing the line segment SP internally. Then
SP=2√5
SQ:QP(√5+1):2
the x-intercept of the normal to the parabola at P is 6
the slope of the tangent to the circle at Q is 12
The correct Answer is:A, C, D
Tangent to y2=4x at (t2,2t) is
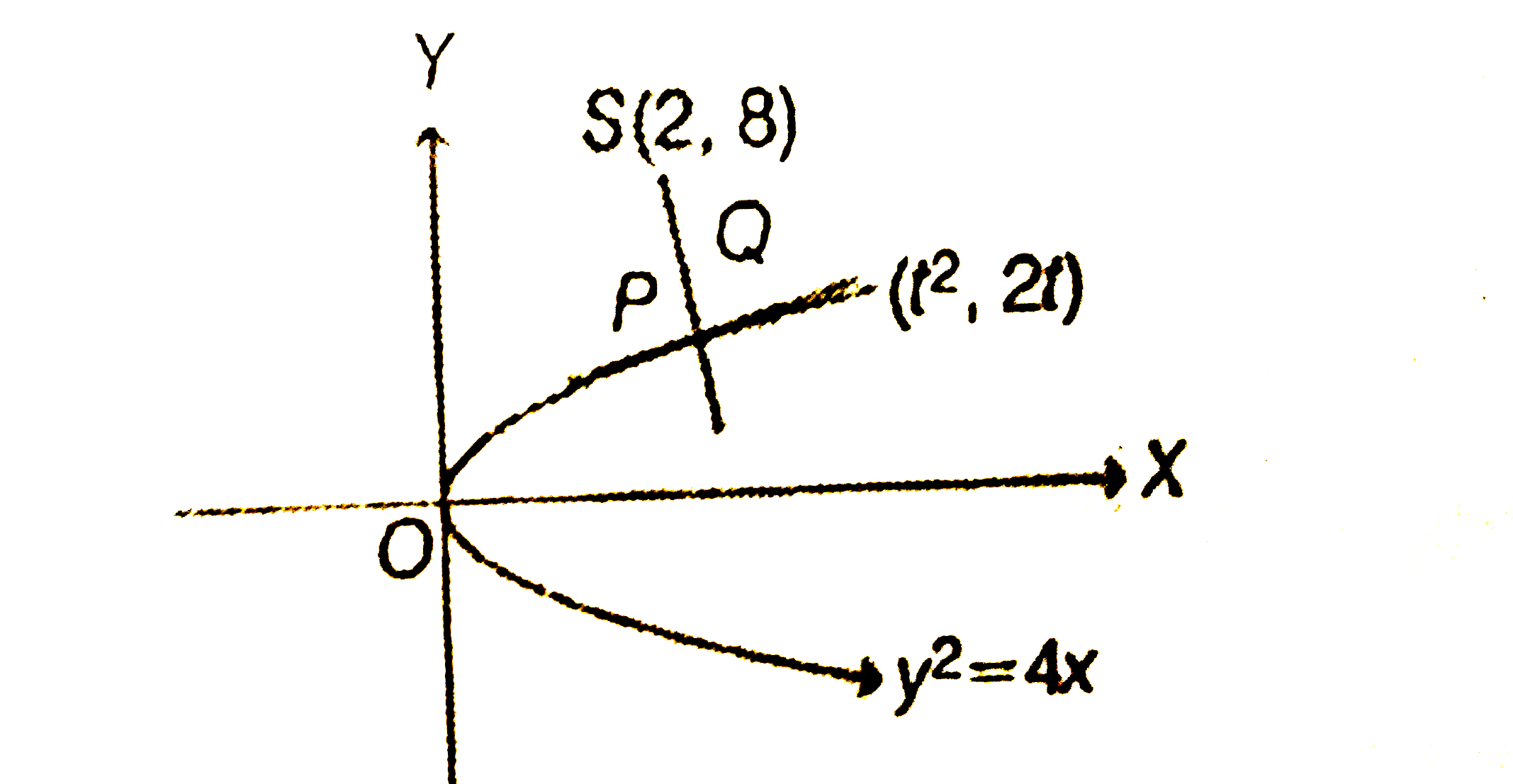
y(2t)=2(x+t2)
⇒yt=x+t2
Equation of normal of P(t2,2t) is
y+tx=2t+t3
Since, normal at P passes through centre of circle S(2,8).
∴8+2t+t3
⇒t=2, i., P (4,4)
[Since, shortest distance between two curves lie along their common normal and the common normal will pass through the centre of circle]
∴SP=√(4−2)2+(4−8)2=2√5
∴ Opion (a) is correct.
Also, SQ=2
∴PQ=SP−SQ=2√5−2
Thus, SQQP=1√5−1=√5+14
∴ Option (b) is wrong
Now x intercept of normal is x=2+22=6
∴ Option (c ) is corect
Slope of tangent =1t=12
∴ Option (d) is correct.
Topper's Solved these Questions
- PARABOLABook:IIT JEE PREVIOUS YEARChapter:PARABOLAExercise:TOPIC 3 EQUATION OF NORMAL AND PROPERTIES OBJECTIVES QUESTIONS II (INTEGER )
Explore 1 Video
- PARABOLABook:IIT JEE PREVIOUS YEARChapter:PARABOLAExercise:TOPIC 3 EQUATION OF NORMAL AND PROPERTIES OBJECTIVES QUESTIONS II (ANALYTICAL & DESCRIPTIVE )
Explore 4 Videos
- PARABOLABook:IIT JEE PREVIOUS YEARChapter:PARABOLAExercise:TOPIC 3 EQUATION OF NORMAL AND PROPERTIES OBJECTIVES QUESTIONS I (MATCH THE COLUMNS )
Explore 1 Video
- MISCELLANEOUSBook:IIT JEE PREVIOUS YEARChapter:MISCELLANEOUSExercise:MISCELLANEOUS
Explore 87 Videos
- PERMUTATIONS AND COMBINATIONSBook:IIT JEE PREVIOUS YEARChapter:PERMUTATIONS AND COMBINATIONSExercise:Dearrangement and Number of Divisors (Fill in the Blank )
Explore 1 Video
Similar Questions
Let P be the point on the parabola y2=4x which is at the shortest distance from the centre S of the circle x2+y2−4x−16y+64=0. Let Q be the point on the circle dividing the lie segment SP internally. Then
View SolutionFind the point on y=x2+4 which is at shortest distance from the line y=4x−4
View Solution
Knowledge Check
Let P be a point on the parabola, x2=4y. If the distance of P from the centre of the circle, x2+y2+6x+8=0 is minimum, then the equation of the tangent to the parabola at P, is:
Ax+4y−2=0Bx+y+1=0Cx−y+3=0Dx+2y=0
The shortest distance from (−2,14) to the circle x2+y2−6x−4y−12=0 is
View SolutionLet P be the point on the parabola, y2=8x which is at a minimum distance from the center C of the circle x2+(y+6)2=1. Then the equation of the circle, passing through C and having its center at P is
View SolutionThe shortest distance from the line 3x+4y=25 to the circle x2+y2=6x−8y is equal to :
View SolutionLet P be the point on the parabola, y2=8x which is at a minimum distance from the centre C of the circle,x2+(y+6)2=1. Then the equation of the circle, passing through C and having its centre at P is : (1) x2+y2−4x+8y+12=0 (2) x2+y2−x+4y−12=0 (3) x2+y2−x4+2y−24=0 (4) x2+y2−4x+9y+18=0
View SolutionFind the greatest distance of the point P(10,7) from the circle x2+y2−4x−2y−20=0
View SolutionLet P be a point on the parabola y2−2y−4x+5=0, such that the tangent on the parabola at P intersects the directrix at point Q. Let R be the point that divides the line segment PQ externally in the ratio 12 : 1. Find the locus of R.
View SolutionFind the shortest distance between the parabola y2=4x and circle x2+y2−24y+128=0.
View Solution

