A simple harmonic wave train is oscillating with 100 vibration/s and has an amplitude of 1 cm. It is progressig along positive X-axis with a velocity of 10 m/s. At x = 150 cm from the orgin and t = 5 s, determine
(i) the displacement
(ii) the particle velocity
(iii) particle acceleration
To solve the problem, we will follow these steps:
Given Data:
- Frequency (f) = 100 vibrations/s = 100 Hz
- Amplitude (A) = 1 cm = 0.01 m
- Wave velocity (v) = 10 m/s
- Position (x) = 150 cm = 1.5 m
- Time (t) = 5 s
Step 1: Find the Wavelength (λ)
The relationship between wave velocity (v), frequency (f), and wavelength (λ) is given by the equation:
v=f⋅λ
Rearranging this gives:
λ=vf
Substituting the known values:
λ=10 m/s100 Hz=0.1 m=10 cm
Step 2: Write the Wave Equation
The general equation for a wave traveling in the positive x-direction is:
y(x,t)=Asin(ωt−kx)
Where:
- ω=2πf (angular frequency)
- k=2πλ (wave number)
Calculating ω and k:
ω=2π⋅100=200π rad/s
k=2π0.1=20π rad/m
Step 3: Substitute Values into the Wave Equation
Now, substituting the values into the wave equation:
y(1.5,5)=0.01sin(200π⋅5−20π⋅1.5)
Calculating the arguments:
200π⋅5=1000π
20π⋅1.5=30π
Thus:
y(1.5,5)=0.01sin(1000π−30π)=0.01sin(970π)
Since sin(970π)=0:
y(1.5,5)=0.01⋅0=0 m
Step 4: Find Particle Velocity
The particle velocity is given by the derivative of the displacement with respect to time:
vy=∂y∂t=Aωcos(ωt−kx)
Substituting the values:
vy=0.01⋅200πcos(1000π−30π)
vy=0.01⋅200πcos(970π)
Since cos(970π)=−1:
vy=0.01⋅200π⋅(−1)=−2π m/s≈−6.283 m/s
Step 5: Find Particle Acceleration
The particle acceleration is given by the second derivative of the displacement with respect to time:
ay=∂2y∂t2=−Aω2sin(ωt−kx)
Substituting the values:
ay=−0.01⋅(200π)2sin(970π)
Since sin(970π)=0:
ay=−0.01⋅(200π)2⋅0=0 m/s2
Final Answers:
(i) Displacement y=0 m
(ii) Particle Velocity vy≈−6.283 m/s
(iii) Particle Acceleration ay=0 m/s2
- Frequency (f) = 100 vibrations/s = 100 Hz
- Amplitude (A) = 1 cm = 0.01 m
- Wave velocity (v) = 10 m/s
- Position (x) = 150 cm = 1.5 m
- Time (t) = 5 s
The relationship between wave velocity (v), frequency (f), and wavelength (λ) is given by the equation:
v=f⋅λ
λ=vf
λ=10 m/s100 Hz=0.1 m=10 cm
The general equation for a wave traveling in the positive x-direction is:
y(x,t)=Asin(ωt−kx)
- ω=2πf (angular frequency)
- k=2πλ (wave number)
ω=2π⋅100=200π rad/s
k=2π0.1=20π rad/m
Now, substituting the values into the wave equation:
y(1.5,5)=0.01sin(200π⋅5−20π⋅1.5)
200π⋅5=1000π
20π⋅1.5=30π
Thus:
y(1.5,5)=0.01sin(1000π−30π)=0.01sin(970π)
y(1.5,5)=0.01⋅0=0 m
The particle velocity is given by the derivative of the displacement with respect to time:
vy=∂y∂t=Aωcos(ωt−kx)
vy=0.01⋅200πcos(1000π−30π)
vy=0.01⋅200πcos(970π)
vy=0.01⋅200π⋅(−1)=−2π m/s≈−6.283 m/s
The particle acceleration is given by the second derivative of the displacement with respect to time:
ay=∂2y∂t2=−Aω2sin(ωt−kx)
ay=−0.01⋅(200π)2sin(970π)
ay=−0.01⋅(200π)2⋅0=0 m/s2
(i) Displacement y=0 m
(ii) Particle Velocity vy≈−6.283 m/s
(iii) Particle Acceleration ay=0 m/s2
Topper's Solved these Questions
- WAVESBook:MODERN PUBLICATIONChapter:WAVESExercise:PROBLEM
Explore 9 Videos
- WAVESBook:MODERN PUBLICATIONChapter:WAVESExercise:PRACTICE PROBLEMS
Explore 38 Videos
- UNITS AND MEASUREMENTBook:MODERN PUBLICATIONChapter:UNITS AND MEASUREMENTExercise:CHAPTER PRACTICE TEST
Explore 15 Videos
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Chapter Practice Test
Explore 16 Videos
Similar Questions
A simple harmonic wave train of amplitude 1 cm and frequency 100 vibration is travelling along positive x-direction with a velocity ov 15ms−1. Calculate displacement y , the particle velocity and particle acceleration at x=180cm from the origin at t=5 s.
View SolutionA simple harmonic wave-train is travelling in a gas in the positive direction of the X-axis.Its amplitude is 2 cm, velocity 45ms−1 and frequency 75s−1.Write down the equation of the wave Find the displacement of the particle of the medium at a distance of 135 cm from the origin in the direction of the wave at the instant t=3 s.
View Solution
Knowledge Check
A particle executes simple harmonic motion with an amplitude of 4 cm . At the mean position the velocity of the particle is 10 cm/ s . The distance of the particle from the mean position when its speed becomes 5 cm/s is
A√3cmB√5cmC2√3cmD2√5cmA particle executes simple harmonic motion with an amplitude of 4 cm. At the mean position, the veloocity of the particles is 10 cm/s. The distance of the particles from the mean position when its speed becomes 5 cm/s is
A√3 cmB√5 cmC2(√3) cmD2(√5) cmA simple harmonic progressive wave has a wavelength 40 cm, periodic time 10 s and zero initial phase. What is the phase of an oscillating particles at a distane of 10 cm form the source at an instant t = 5s ?
Aπ6 radianBπ4 radianCπ3 radianDπ2 radian
A particle is moving along the x-axis. Consider it’s a-t graph. If initial velocity is 10 m//s, sketch the v-t graph and calculate the displacement in the time interval t=0 to 12 s.
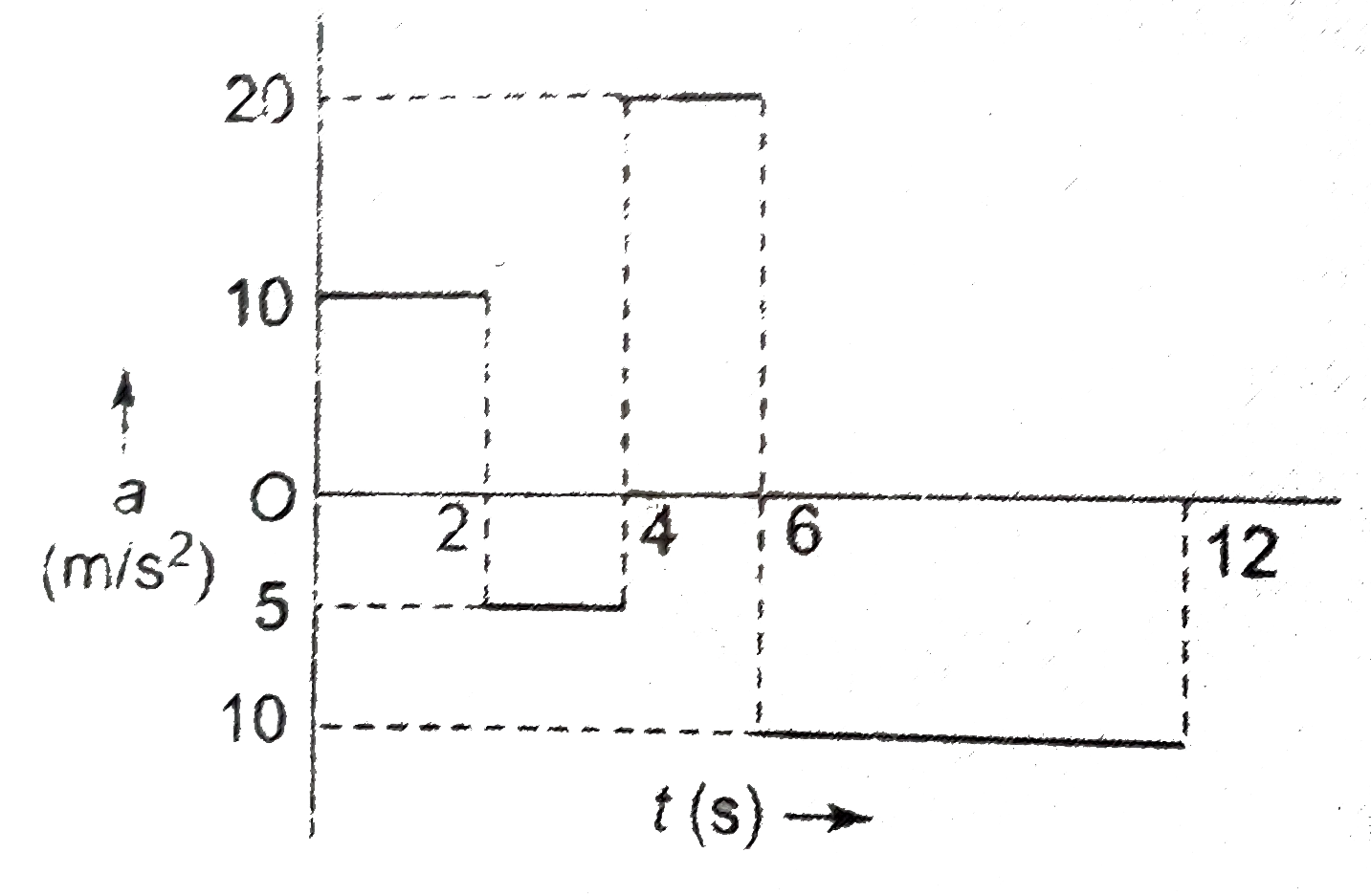
View SolutionA particle executes simple harmonic motion with an amplitude of 10cm and time period 6s. At t=0 it is position x=5cm from mean postion and going towards positive x−direaction. Write the equation for the displacement x at time L. Find the magnitude of the acceleration of the particle at t=4s.
View SolutionA simple harmonic wave of amplitude 8 units travels along positive x-axis. At any given instant of time, for a particle at a distance of 10cm from the origin, the displacement is +6units, and for a particle at a distance of 25cm from the origin, the displacement is +4 units. Calculate the wavelength.
View SolutionA particle executes simple harmonic motion with an amplitude of 10 cm and time period 6s. Ast t=0 it is at position x=5 cm going towasrds positive x-direction. Write the eqwuation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t=4s.
View SolutionChoose the most appropriate option.
A simple harmonic wave of amplitude 8 unit travels along positive x-axis. At any given instant of time, for a particle at a distance of 10 cm from the origin, the displacement is + 6 unit and for a particle at a distance of 25 cm from the origin, the displacement is + 4 unit. Calculate the wavelength.
View Solution

