A simple harmonic wave-train is travelling in a gas in the positive direction of the X-axis.Its amplitude is 2 cm, velocity 45ms−1 and frequency 75s−1.Write down the equation of the wave Find the displacement of the particle of the medium at a distance of 135 cm from the origin in the direction of the wave at the instant t=3 s.
The correct Answer is:y=2sin2π(75t−x60), -2 cm
To solve the problem step by step, we will follow these steps:
Step 1: Write down the given parameters
- Amplitude (A) = 2 cm = 0.02 m (convert to meters for consistency)
- Velocity (v) = 45 m/s
- Frequency (f) = 75 Hz
Step 2: Calculate the period (T) of the wave
The period T is the reciprocal of the frequency:
T=1f=175 s≈0.01333 s
Step 3: Calculate the wavelength (λ)
The wavelength λ can be calculated using the formula:
λ=vf=45 m/s75 Hz=0.6 m
Step 4: Write the wave equation
The general form of the wave equation for a wave traveling in the positive x-direction is:
y(x,t)=Acos(2π(tT−xλ))
Substituting the values we have:
y(x,t)=0.02cos⎛⎝2π⎛⎝t175−x0.6⎞⎠⎞⎠
Step 5: Substitute the values into the wave equation
We need to find the displacement y at x=135 cm=1.35 m and t=3 s:
y(1.35,3)=0.02cos(2π(75⋅3−1.350.6))
Step 6: Calculate the argument of the cosine function
First, calculate 1.350.6:
1.350.6=2.25
Now calculate 75⋅3:
75⋅3=225
Thus, the argument becomes:
2π(225−2.25)=2π(222.75)
Step 7: Evaluate the cosine
Now we evaluate:
y(1.35,3)=0.02cos(2π⋅222.75)
Since cos(2πn)=1 for any integer n, we need to find the fractional part:
222.75 is approximately 223 (an integer)+0.75
Thus:
cos(2π⋅0.75)=cos(3π2)=0
So:
y(1.35,3)=0.02⋅0=0
Conclusion
The displacement of the particle of the medium at a distance of 135 cm from the origin at the instant t=3 s is:
0 m
- Amplitude (A) = 2 cm = 0.02 m (convert to meters for consistency)
- Velocity (v) = 45 m/s
- Frequency (f) = 75 Hz
The period T is the reciprocal of the frequency:
T=1f=175 s≈0.01333 s
The wavelength λ can be calculated using the formula:
λ=vf=45 m/s75 Hz=0.6 m
The general form of the wave equation for a wave traveling in the positive x-direction is:
y(x,t)=Acos(2π(tT−xλ))
Substituting the values we have:
y(x,t)=0.02cos⎛⎝2π⎛⎝t175−x0.6⎞⎠⎞⎠
We need to find the displacement y at x=135 cm=1.35 m and t=3 s:
y(1.35,3)=0.02cos(2π(75⋅3−1.350.6))
First, calculate 1.350.6:
1.350.6=2.25
Now calculate 75⋅3:
75⋅3=225
Thus, the argument becomes:
2π(225−2.25)=2π(222.75)
Now we evaluate:
y(1.35,3)=0.02cos(2π⋅222.75)
Since cos(2πn)=1 for any integer n, we need to find the fractional part:
222.75 is approximately 223 (an integer)+0.75
Thus:
cos(2π⋅0.75)=cos(3π2)=0
So:
y(1.35,3)=0.02⋅0=0
The displacement of the particle of the medium at a distance of 135 cm from the origin at the instant t=3 s is:
0 m
Topper's Solved these Questions
Similar Questions
A wave is propagating along the positive direction of X-axis. If the amplitude of wave is 10 cm, frequency 200 Hz and velocity 400 m/s, then write the equation of progressive wave.
View SolutionA plane progressive wave is propagating along positive direction of X-axiss where frequency is 100 Hz, amplitude is 20 cm and velocity is 300 m/s. Find the equation of wave.
View Solution
Knowledge Check
A travelling wave in the gas along the positive x-direction has an amplitude of 2cm, velocity 45m/s and frequency 75Hz. Particle acceleration after an interval of 3 sec at a distance of 135cm from the origin is
A0.44×102cm/s2B4.4×105cm/s2C4.4×103cm/s2D44×105cm/s2A progressive wave is travelling along the positive direction of the x-axis. For this wave, amplitude = 5 cm, period = 0.2 s and wavelength = 30 cm
The equation of the wave using SI units is given byAy=0.05sin2π(t0.2−x0.3)By=0.5sin2π(t0.2−x30)Cy=5sin2π(t0.2+x3)Dy=0.05sin2π(x0.3+t0.2)A simple harmonic progressive wave of frequency 100 Hz is travelling along the positive direction of the X axis. What is the propagation constant, if the velocity of the wave is 500 m/s ?
A2π5 per metreBπ5 per metreC2π3 per metreD32π per metre
A sinusoidal wave travelling in the positive x direction has an amplitude of 15 cm, wavelength 40 cm and frequency 8 Hz. The vertical displacement of the medium at t =0 and x = 0 is also 15 cm, as shown
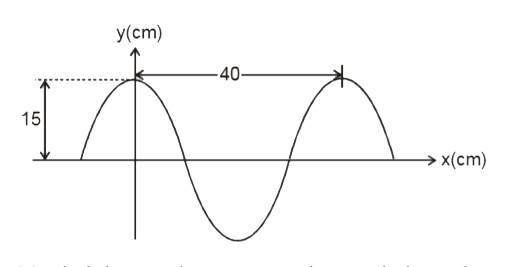
(b) Determine the phase constant ϕ, and write a general expression for the wave function.
View SolutionA longitudinal harmonic wave is travelling along positive x direction. The amplitude, wavelength and frequency of the wave are 8.0×10–3m,12cm and 6800Hz respectively. The displacement (s) versus position graph for particles on the x axis at an instant of time has been shown in figure. Find the separation at the instant shown, between the particles which were originally at x1=1cm and x2=3cm

View SolutionA sinusoidal wave travelling in the positive x direction has an amplitude of 15 cm, wavelength 40 cm and frequency 8 Hz. The vertical displacement of the medium at t =0 and x = 0 is also 15 cm, as shown
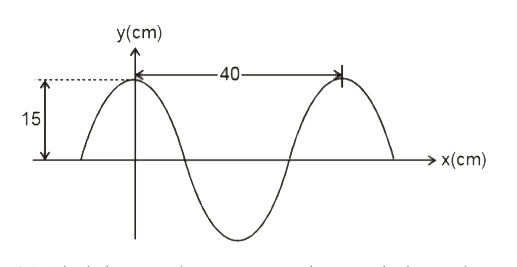
(a) Find the angular wave number, period angular frquency and speed of the wave.
View SolutionThe consitutent waves of a stationary wave on a string fixed at two ends are amplitude 6 cm, frequency 50Hz and velocity 80cms−1. Write down the equation of stationary wave.
View SolutionThe equation of progressive wave travelling a long positive direction of x axis having a amplitude of 0.04 m, frequency 440 Hz and wave velocity 330 m/s, is
View Solution
