In a photoelectric tube, the voltage applied is such that the photoelectrons emitted reverse in direction after traveling half the distance. we keep the voltage same but halve the distance, then
The photoelectrons reverse the direction at half of the new distance
The photoelectrons are just able to reach the other electrode
The photoelectrons reverse the direction at one fourth of the new distance
The photoelectrons reach the other electrode with some kinetic energy
The correct Answer is:B
To solve the problem, we need to analyze the situation in a photoelectric tube where photoelectrons are emitted and influenced by an electric field. Let's break it down step by step.
Step 1: Understand the Initial Setup
In the photoelectric tube, we have a metal target where electromagnetic waves (light) are incident. When these waves hit the metal, electrons absorb energy and are emitted from the surface. The emitted electrons have some kinetic energy and start moving towards a positively charged plate.
Hint: Remember that photoelectrons are emitted due to the absorption of energy from incident light.
Step 2: Analyze the Electric Field
The setup includes two plates: one positively charged and the other negatively charged. The electric field is directed from the positive plate to the negative plate. When the photoelectrons are emitted, they experience a force due to this electric field.
Hint: The direction of the electric field affects the motion of the electrons.
Step 3: Motion of Photoelectrons
Initially, the photoelectrons travel towards the positive plate. However, due to the negative charge of the plate they are moving towards, they experience a force in the opposite direction, which slows them down. The problem states that they reverse direction after traveling half the distance.
Hint: Consider the effect of the electric field on the kinetic energy of the electrons.
Step 4: Halving the Distance
Now, we keep the voltage (and thus the electric field strength) the same but halve the distance between the plates. This means the distance the electrons have to travel is reduced.
Hint: Think about how reducing the distance affects the time and distance the electrons travel before they are influenced by the electric field.
Step 5: Analyze the New Situation
Since the electric field strength remains unchanged and the kinetic energy of the emitted electrons is the same, the electrons will still experience the same retardation force. However, because the distance is halved, they will not travel as far before the force acts on them.
Hint: The electrons will still experience the same force, but they will have less distance to travel before being affected.
Step 6: Conclusion
In this new setup, the photoelectrons will just be able to reach the other plate before reversing direction. This means they will travel a shorter distance and will still be influenced by the electric field, causing them to stop and reverse direction after reaching the new position.
Final Answer: The photoelectrons will just be able to reach the other plate before reversing direction.
Summary of Steps:
1. Understand the initial setup of the photoelectric tube.
2. Analyze the electric field created by the charged plates.
3. Consider the motion of the photoelectrons and the effect of the electric field.
4. Halve the distance between the plates while keeping the voltage the same.
5. Conclude that the photoelectrons will just reach the other plate before reversing direction.
In the photoelectric tube, we have a metal target where electromagnetic waves (light) are incident. When these waves hit the metal, electrons absorb energy and are emitted from the surface. The emitted electrons have some kinetic energy and start moving towards a positively charged plate.
The setup includes two plates: one positively charged and the other negatively charged. The electric field is directed from the positive plate to the negative plate. When the photoelectrons are emitted, they experience a force due to this electric field.
Initially, the photoelectrons travel towards the positive plate. However, due to the negative charge of the plate they are moving towards, they experience a force in the opposite direction, which slows them down. The problem states that they reverse direction after traveling half the distance.
Now, we keep the voltage (and thus the electric field strength) the same but halve the distance between the plates. This means the distance the electrons have to travel is reduced.
Since the electric field strength remains unchanged and the kinetic energy of the emitted electrons is the same, the electrons will still experience the same retardation force. However, because the distance is halved, they will not travel as far before the force acts on them.
In this new setup, the photoelectrons will just be able to reach the other plate before reversing direction. This means they will travel a shorter distance and will still be influenced by the electric field, causing them to stop and reverse direction after reaching the new position.
1. Understand the initial setup of the photoelectric tube.
2. Analyze the electric field created by the charged plates.
3. Consider the motion of the photoelectrons and the effect of the electric field.
4. Halve the distance between the plates while keeping the voltage the same.
5. Conclude that the photoelectrons will just reach the other plate before reversing direction.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - PHOTONS AND MATTER WAVESEXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type)5videos
PHOTONS AND MATTER WAVES
- BOOK - RESNICK AND HALLIDAYCHAPTER - PHOTONS AND MATTER WAVESEXERCISE - PRACTICE QUESTIONS (Link Comprehension)17videos
PHOTONS AND MATTER WAVES
- BOOK - RESNICK AND HALLIDAYCHAPTER - PHOTONS AND MATTER WAVESEXERCISE - PROBLEMS50videos
PHOTONS AND MATTER WAVES
- BOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Practice Questions57videos
OSCILLATIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Integer Type)5videos
RELATIVITY
Similar Questions
While travelling towards goa from Mumbai, Ganesh saw milestone with two digits indicating the distance of that point from Mumbai. After travelling some distance, he saw another milestone with the same digits but in reverse order. Further travelling the same distance that he had travelled from the 1st milestone to the 2nd milestone, he saw another milestone with a 3-digit number that had the same digits but also had a zero in it. But the order of the digits was different. His speed was uniform through out the journey. The distance between the 3rd and 1st milestone is :
View SolutionCase study :
Read the following paragraph and answers the questions :
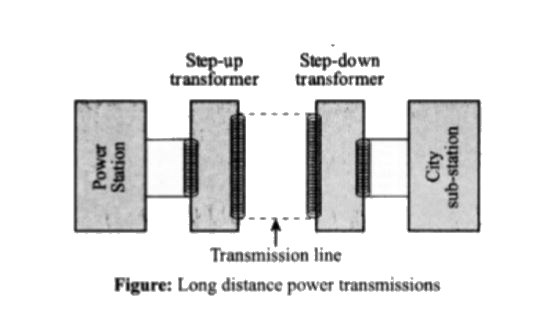
The large-scale transmission and distribution of electrical energy over long distances is done with the use of transformers. The voltage output of the generator is stepped-up. It is then transmitted over long distances to an area sub-station near the consumers. There the voltage is stepped down. It is further stepped down at distributing sub-stations and utility poles before a power supply of 240 V reaches our homes.
We need to step-up the voltage for power transmission, so thatView Solution
Knowledge Check
- Question 1 - Select One or More
In an X-ray tube, the voltage applied is 20kV. The energy required to remove an electron fromLshellis19.9keV In the X-rays emitted by the tube.
Aminimum wavelength will be 62.1nm.Benergy of the characteristic x-rays will be equal to oe less than 19.9keV.CLα X-ray may be emitted.DLα X-ray will have energy 19.9keV. - Question 2 - Select One
A particle moves so that s=6+48t-t3. The direction of motion reverses after moving a distance of
A63B104C134D288 - Question 3 - Select One
A particle moves so that x=2+27t-t3. The direction of motion reverses after moving a distance of . . . Units.
A80B56C60D65
Consider the previous problem
(a) When does the particle reach A again?
(b) Locate the point where the particle reverses its direction of motion.
(c) Find the distance travelled by the particle in the first 15 seconds.View SolutionThe photoelectric cut off voltage in a certain experiment is 1.5V. What is the maximum kinetic energy of photoelectrons emitted? e=1.6×10−19C.
View SolutionThe photoelectric cut-off voltage in a certain experiment is 1.5 V. what is the maximum kinetic energy of photoelectrons emitted ?
View SolutionA body of mass m is travelling with a velocity vu. When a constant retarding force F is applied, it comes to rest after travelling a distance s1. If the initial velocity is 2u with the same force F, the distance travelled before it comes to rest is s2. then,
View Solution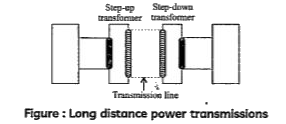
Figure : Long distance power transmissions The large-scale transmission and distribution of electrical energy over long distances is done with the use of transformers. The voltage output of the generator is stepped-up. It is then transmitted over long distances to an area sub station near the consumers. There the voltage is stepped down. It is further stepped down at distributing sub-stations and utility poles before a power supply of 240 V reaches our homes.
We need to step-up the voltage for power. transmission, so that:View Solution
