A particle of mass m=1.6×10−27 kg and charge q=1.6×10−19C enters a region of uniform magnetic field of stregth 1T along the direction shown in figure. The speed of the particle is 107m/s

a. The magnetic field is directed along the inward normal to the plane of the paper. The particle leaves the region of the fiedl at the point F. Find the distasnce EF and the angle theta.
b. If the direction of the field is along the outward normal to the plane of the paper find the time spent by the particle in the regin of the magnetic field after entering it at E.
First of all let us see how the path look like. At least for the part when the particle is inside the magnetic field, the path will be part of a circle. To locate the center, let us find the direction of q(→v×→B).
As can be seen in the figure, it is directed perpendicular to velocity and is toward O. Since this force is centripetal in nature, the force is directed toward the center. The coordinates of center can be easily found out. The charge particle will move in anticlockwise direction and exit the magnetic field at the boundary.
When a charged particle moves perpendicular to a magnetic field the path is a circle with magnetic force qvB directed radially toward the center of the path. So, if we draw normal at E and F they will meet at O which is the center of the circle. By geometry of Fig.
θ=ϕ2=ϕ1=45∘
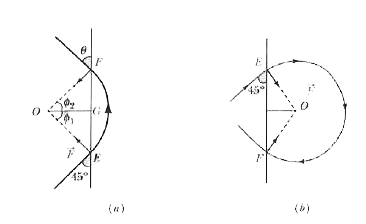
Calculation : As ϕ1=ϕ2=θ, therefore
EF=2EG=2rsinθ.
Since
r=mvqB=1.6×10−27×1071.6×10−19×1=0.1m,
therefore
EF−(2×0.1×sin45∘)m=10√2cm.
Now, as in a magnetic field the speed of a particle remains constant, so if t is the time taken by the particle in the field, then
S=v×t=rθ
t=rθv.
Hence,
t=0.1×π/2107=5π×10−9=1.57×10−8s.
Topper's Solved these Questions
- MAGNETIC FORCEBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FORCEEXERCISE - Check point
6 Videos
- MAGNETIC FORCEBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FORCEEXERCISE - Problems
49 Videos
- MAGNETIC FIELDS DUE TO CURRENTSBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Practice Question (Integer Type)
4 Videos
- MOTION ALONG A STRAIGHT LINEBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Integer Type )
3 Videos
Similar Questions
A particle of mass m=1.6×1027 kg and charge q=1.6×10−19 C moves at a speed of 1.0×107ms−7. It enters a region of uniform magnetic field at a point E, as shown in The field has a strength of 1.0 T. (a) The magnetic field is directed into the plane of the paper. The particle leaves the region of the filed at the point F. Find the distance EF and the angle theta. (b) If the field is coming out of the paper, find the time spent by the particle in the region of the magnetic field after entering it at E.

View SolutionFour particles enter a region of uniform magnetic field. Their trajectories are shown in figure. What are the signs of the charge of all four particles ?
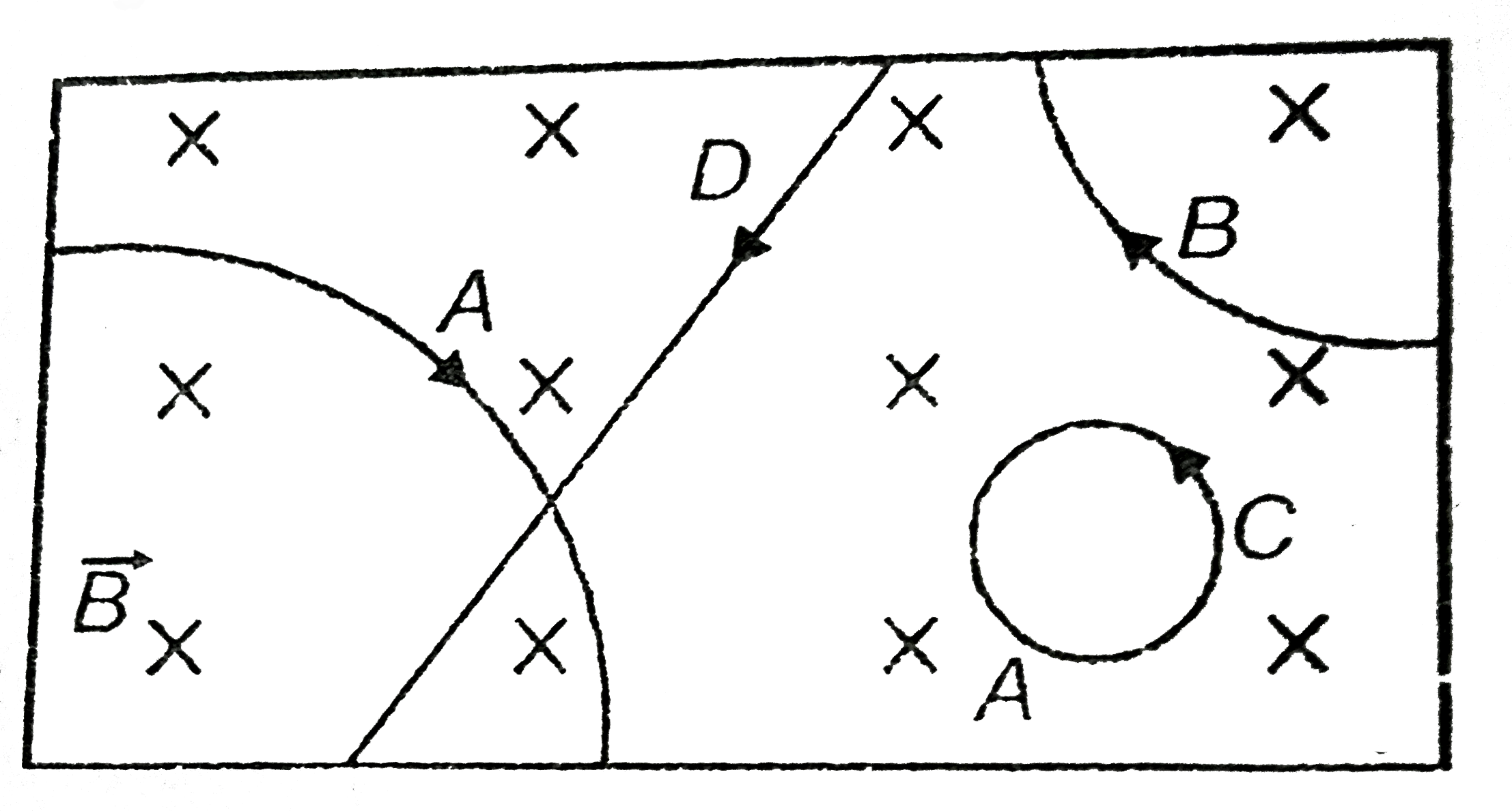
View Solution
Knowledge Check
A particle of mass 1.6×10−27kg and charge 1.6×10−19 coulomb enters a uniform magnetic field of 1 Tesla as shown in the figure. The speed of the particle is 107m/s. The distance PQ will be
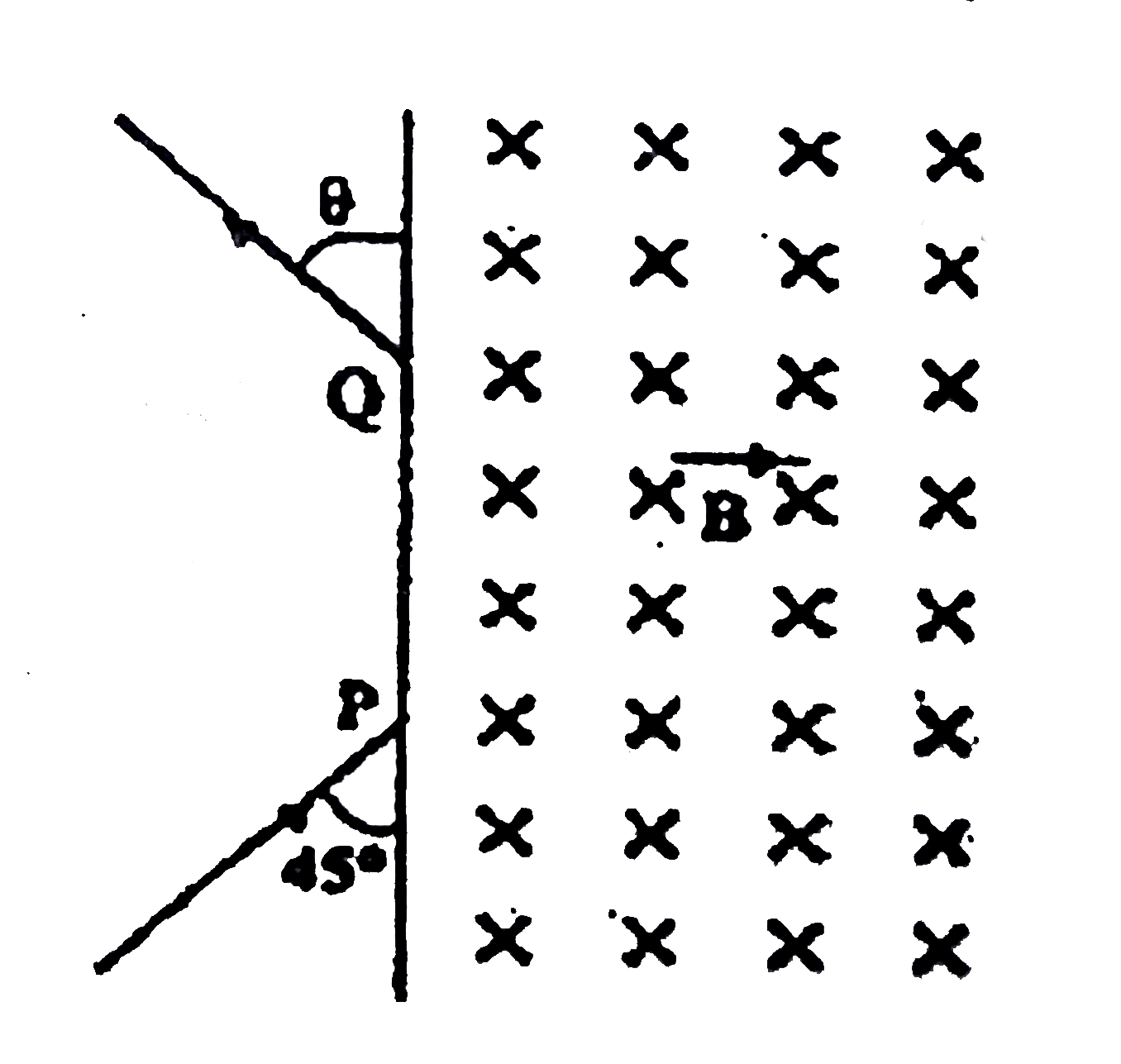 A0.14 mB0.28 mC0.4 mD0.5 m
A0.14 mB0.28 mC0.4 mD0.5 mA particle enters the region of a uniform magnetic field as shown in figure. The path of the particle inside the field is shown by dark line. The particle is :
 Aelectrically neutralBpositively chargedCnegatively chargedDinformation given is inadequate
Aelectrically neutralBpositively chargedCnegatively chargedDinformation given is inadequateA small particle of mass m = 1 kg and charge of 1C enters perpendicularly in a triangular region of uniform magnetic field of strength 2T as shown in figure :
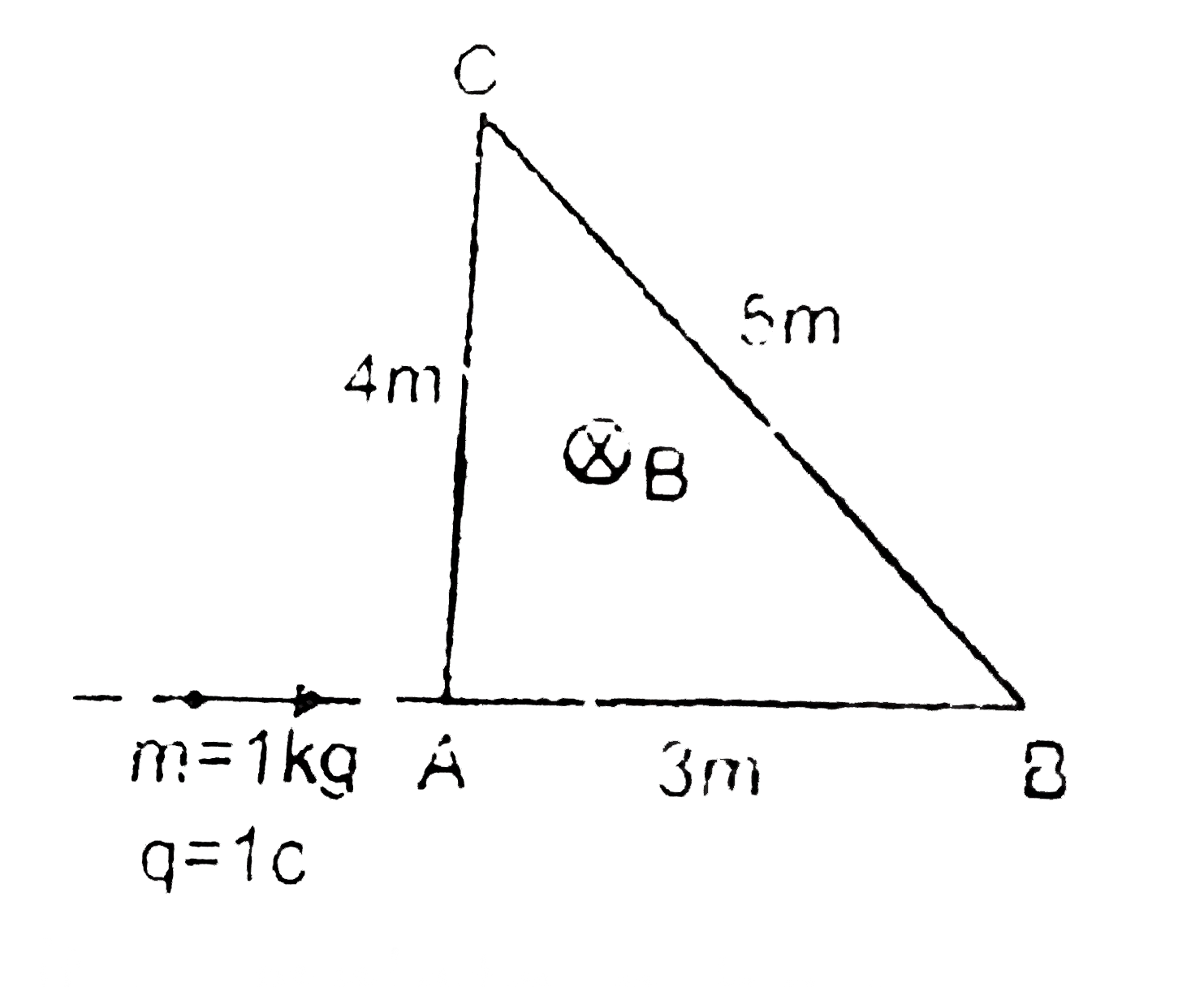
Calculate maximum velocity of the particle with which it should enter so that it complete a half-circle in magnetic region :A2 m/sB2.5 m/sC3 m/sD4 m/s
A proton of mass 1.67×10−27 kg and charge 1.6×10−19C is shot a uniform magnetic field, and perpendicular to the field with a velocity 5×106m/s. If the magnetic induction of the field is 1 tesla, find
(i) The radius of the circular path
View SolutionA neutron, a proton, an electron and an a-particle enters a uniform magnetic field with equal velocities. The field is directed along the inward normal to the plane of the paper. Which of these tracks followed are by a - particle.
View SolutionParticles of mass 1.6×10−27 kg and charge 1.6×10−19C are accelerated in a cyclotron of dee radius 40cm. It employs a magnetic field 0.4T. Find the kinetic energy (in MeV) of the particle beam imparted by the accelerator.
View SolutionA particle of mass m and charge +q enters a region of magnetic field with a velocity v, as shown in Fig. 1.93.
a. Find the angle subtended by the circular arc described by it in the magnetic field.
b. How long does the particle stay inside the magnetic field?
c. If the particle enters at E, what is the intercept EF?

View SolutionA particle of mass 6.4×10−27 kg and charge 3.2×10−19C is situated in a uniform electric field of 1.6×105Vm−1. The velocity of the particle at the end of 2×10−2m path when it starts from rest is :
View Solution
