A particle of mass m and charge +q enters a region of magnetic field with a velocity v, as shown in Fig. 1.93.
a. Find the angle subtended by the circular arc described by it in the magnetic field.
b. How long does the particle stay inside the magnetic field?
c. If the particle enters at E, what is the intercept EF?

(a) The particle circulates under the influence of magnetic field. As the magnetic field is uniform , the charge comes out symmetrically. The angle subtended at the centre is (180−2θ).
(b) The length of the arc traced by the particle, l=R(π−2θ)
Time spent in the field, t=lv=R(π−2θ)v and R=mvBq
which gives t=mBq(π−2θ)
As time period: T=2πmBq, hence t=T2π(π−2θ)

we can generalize this result, If ϕ is the angle subtended by the arc traced by the charged particle is the magnetic field, the time spent is t=T(ϕ2π)
(c) Intercept EF=2Rcosθ.
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.1
22 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.2
13 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
- KINETIC THEORYBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORYEXERCISE - Question Bank
31 Videos
- Magnetism and MatterBOOK - CENGAGE PHYSICSCHAPTER - Magnetism and MatterEXERCISE - Question Bank
50 Videos
Similar Questions
A particle of mass m and positive charge q,moving with a uniform velocity v enters a magnetic field B as shown in figure.(a) Find the radius of the circular arc it describes in the magnetic field. (b)Find the angle subtended by the arc at the centre. (c) How long does the particle stay inside the magnetic field? (d)Solve the three parts of the above problem if the charge q on the particle is negative.
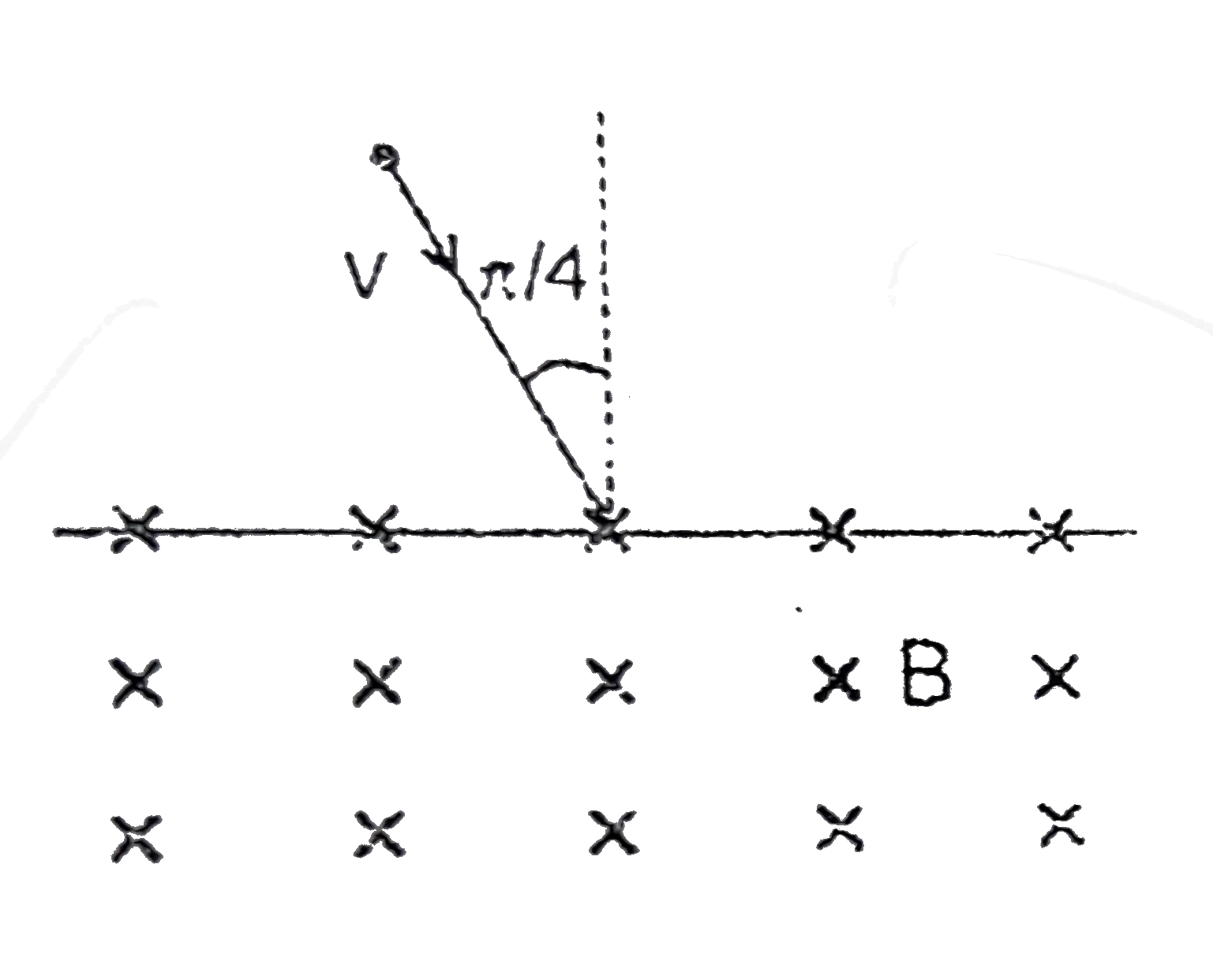
View SolutionA particle of mass m and positive charge q, moving with a uniform velocity v, enters a magnetic field B as shown in Find The radius of the circular are it describes in the magnetic field. (b) find the angle subtended by the arc at the centre. (c ) How long does the particle stay inside the magnetic field? (d) Solve the three parts of the above problem if the charge q on the particle is negative.
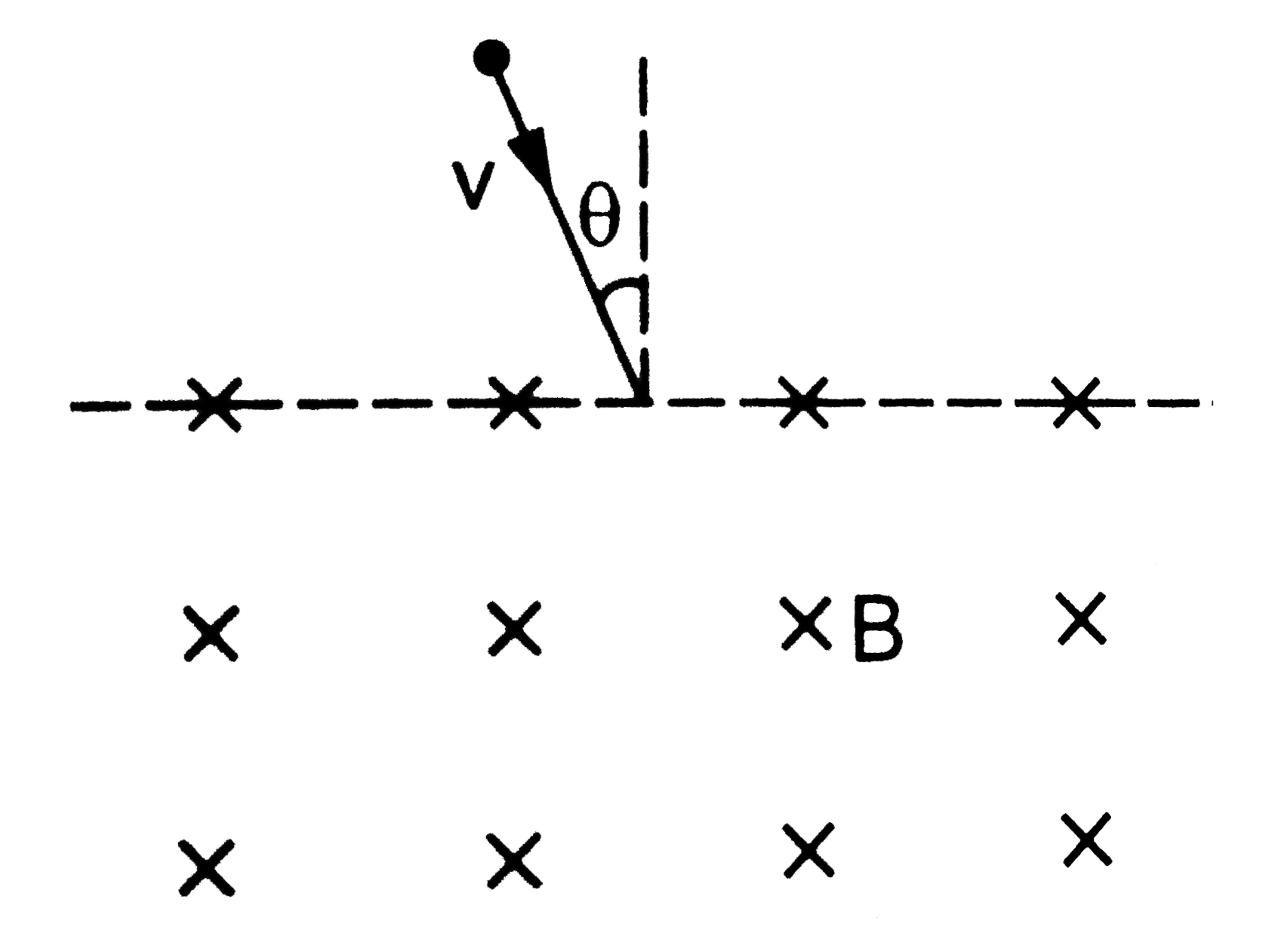
View Solution
Knowledge Check
A particle of mass m and charge q enters a magnetic field B perpendicularly with a velocity v, The radius of the circular path described by it will be
ABq/mvBmq/BvCmB/qvDmv/BqA charged particle of mass m and charge q enters a magnetic field B with a velocity v at an angle θ with the direction of B. The radius fo the resulting path is
AmvsinθqBBmvqBsinθCmvqBDmvtanθqBA charged particle enters into a uniform magnetic field the parameter that remains constant is
AvelocityBmomentumCkinetic energyDangular velocity
A positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find
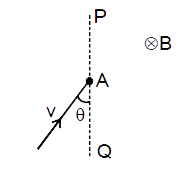
distance travelled in the magnetic field
View SolutionA positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find
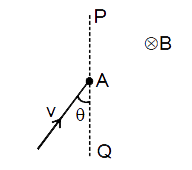
impulse of magnetic force.
View SolutionWhen a charged particle enters a uniform magnetic field its kinetic energy
View SolutionWhen a charged particle enters a uniform magnetic field its kinetic energy
View SolutionA particle of mass m and charge q enters a region of magnetic field (as shown) with speed v at t = 0. There is a region in which the magnetic field is absent as shown. The particle after entering the region collide elastically with a rigid wall. Time t after which the velocity of particle become antiparallel to its initial velocity is -

View Solution
