A proton of mass 1.67×10−27 kg and charge 1.6×10−19C is shot a uniform magnetic field, and perpendicular to the field with a velocity 5×106m/s. If the magnetic induction of the field is 1 tesla, find
(i) The radius of the circular path
To find the radius of the circular path of a proton moving in a magnetic field, we can use the following formula derived from the balance of centripetal force and magnetic force:
r=mvqB
Where:
- r = radius of the circular path
- m = mass of the proton
- v = velocity of the proton
- q = charge of the proton
- B = magnetic field induction
Given Data:
- Mass of the proton, m=1.67×10−27kg
- Charge of the proton, q=1.6×10−19C
- Velocity of the proton, v=5×106m/s
- Magnetic field induction, B=1T
1. Substitute the values into the formula:
r=(1.67×10−27kg)×(5×106m/s)(1.6×10−19C)×(1T)
2. Calculate the numerator:
Numerator=1.67×10−27×5×106=8.35×10−21kg m/s
3. Calculate the denominator:
Denominator=1.6×10−19×1=1.6×10−19C T
4. Now, divide the numerator by the denominator:
r=8.35×10−211.6×10−19=0.0521875m
5. Convert to centimeters (if needed):
r≈5.22cm
Final Answer:
The radius of the circular path is approximately 0.0522m or 5.22cm.
- r = radius of the circular path
- m = mass of the proton
- v = velocity of the proton
- q = charge of the proton
- B = magnetic field induction
- Mass of the proton, m=1.67×10−27kg
- Charge of the proton, q=1.6×10−19C
- Velocity of the proton, v=5×106m/s
- Magnetic field induction, B=1T
r=(1.67×10−27kg)×(5×106m/s)(1.6×10−19C)×(1T)
Numerator=1.67×10−27×5×106=8.35×10−21kg m/s
Denominator=1.6×10−19×1=1.6×10−19C T
r=8.35×10−211.6×10−19=0.0521875m
r≈5.22cm
The radius of the circular path is approximately 0.0522m or 5.22cm.
Similar Questions
A proton of mass 1.67×10−27 kg and charge 1.6×10−19C is shot a uniform magnetic field, and perpendicular to the field with a velocity 5×106m/s. If the magnetic induction of the field is 1 tesla, find
(ii) The frequency of revolution.
View SolutionA cyclotron, when being used to accelerate protons (mass = 1.67×10−27kg, charge = 1.6×10−19C) has a magnetic field of π2 tesla applied normal to the plane of its does. What must be the value of the frequency of the applied alternating electric field to be used in it?
View Solution
Knowledge Check
A proton (mass=1.67×10−27kg and charge 1.6×10−19C) enters perpendicular to a magentic field of intensity 2weber/m2 with a speed of 2.6×107m/sec. The acceleration of the proton should be
A6.5×1015m/sec2B6.5×1013m/sec2C6.5×1011m/sec2D6.5×109m/sec2A particle of mass 1.6×10−27kg and charge 1.6×10−19 coulomb enters a uniform magnetic field of 1 Tesla as shown in the figure. The speed of the particle is 107m/s. The distance PQ will be
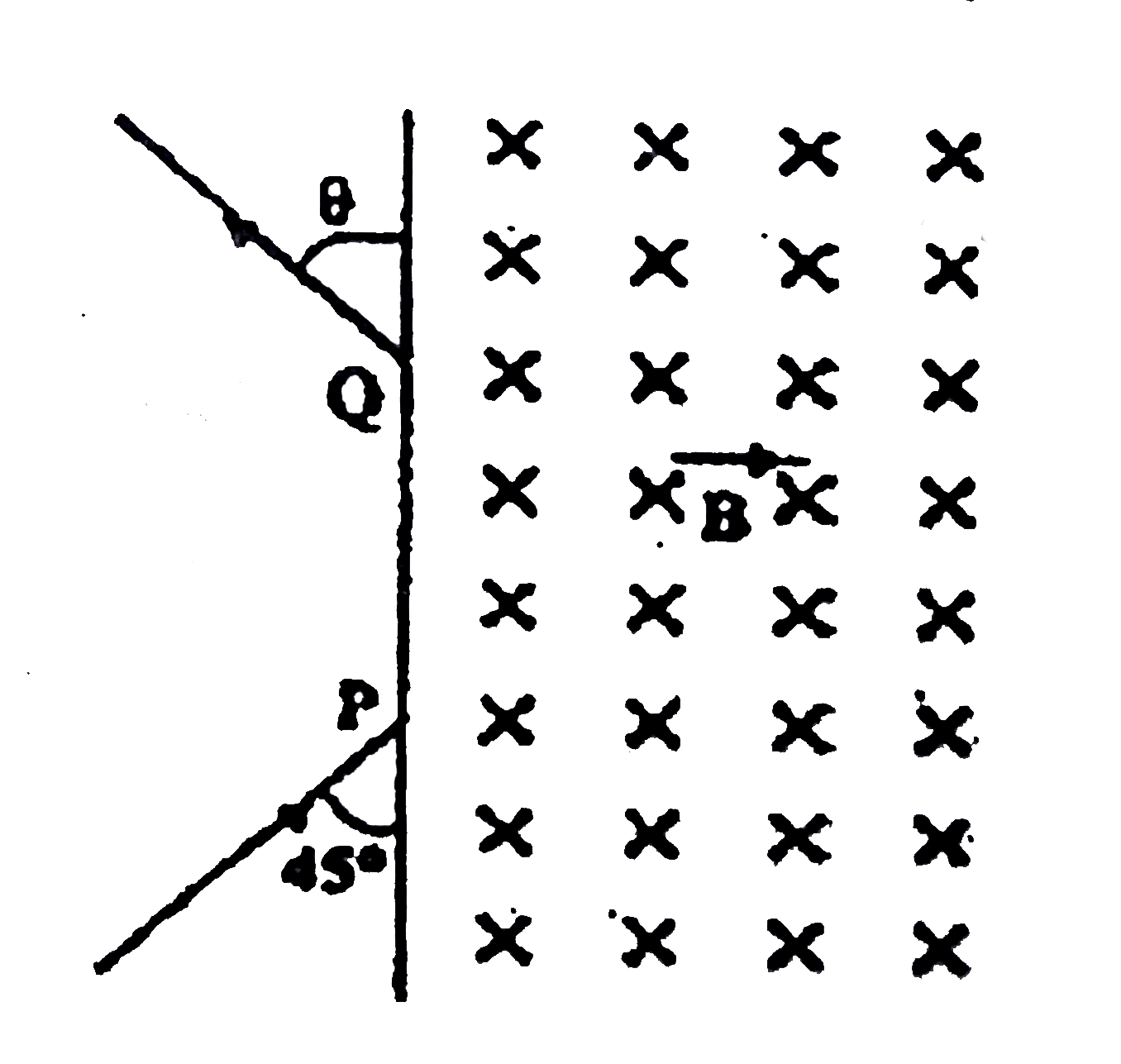 A0.14 mB0.28 mC0.4 mD0.5 m
A0.14 mB0.28 mC0.4 mD0.5 mA proton (mass=1.67×10−27kg and charge 1.6×10−19C) enters perpendicular to a magentic field of intensity 2weber/m2 with a speed of 2.6×107m/sec. The acceleration of the proton should be
A6.5×1015m/sec2B6.5×1013m/sec2C6.5×1011m/sec2D6.5×109m/sec2
An electron having mass (9.1×10−31kg) and charge (1.6×10−19C) moves in a circular path of radius 0.5 m with a velocity 106m/s in a magnetic field. Strength of magnetic field is
View SolutionA particle of mass 6.4×10−27 kg and charge 3.2×10−19C is situated in a uniform electric field of 1.6×105Vm−1. The velocity of the particle at the end of 2×10−2m path when it starts from rest is :
View SolutionA proton of mass 1.67×10−27 kg charge 1.6×10−19C is projected in xy-plane with a speed of 2×106m/s at an angle of 60∘ to the X-axis. If a uniform magnetic field of 0.14 T is applies along the Y-axis, then the path of the proton is
View SolutionA proton of mass 1.67×10−27kg and charge 1.6×10−19c is projected with a speed of 2×106m/s at an angle of 60∘ to the x-axis. If a uniform magnetic field of 0.104 Tesla is applied along Y-axis, the path of proton is
View SolutionElectrons move at right angles to a magnetic field of 1.5×10−2 Tesla with a speed of 6×107m/s. If the specific charge of the electron is 1.7×1011C/kg. The radius of the circular path will be
View Solution

