A ray of light is incident along a line which meets another line, 7x−y+1=0, at the point (0, 1). The ray isthen reflected from this point along the line, y+2x=1. Then the equation of the line of incidence of the ray of light is (A) 41x+38y−38=0 (B) 41x−38y+38=0 (C) 41x+25y−25=0 (D) 41x−25y+25=0
41x + 38y - 38 = 0
41 x - 38y + 38 = 0
41x + 25y - 25 = 0
41 x - 25y + 25 = 0
The correct Answer is:B
The line along the incident ray passes through the intersection of the lines 7x−y+1=0 and 2x + y - 1 = 0 . Let its equation be
7x−y+1+λ(2x+y−1)=0 …(i)
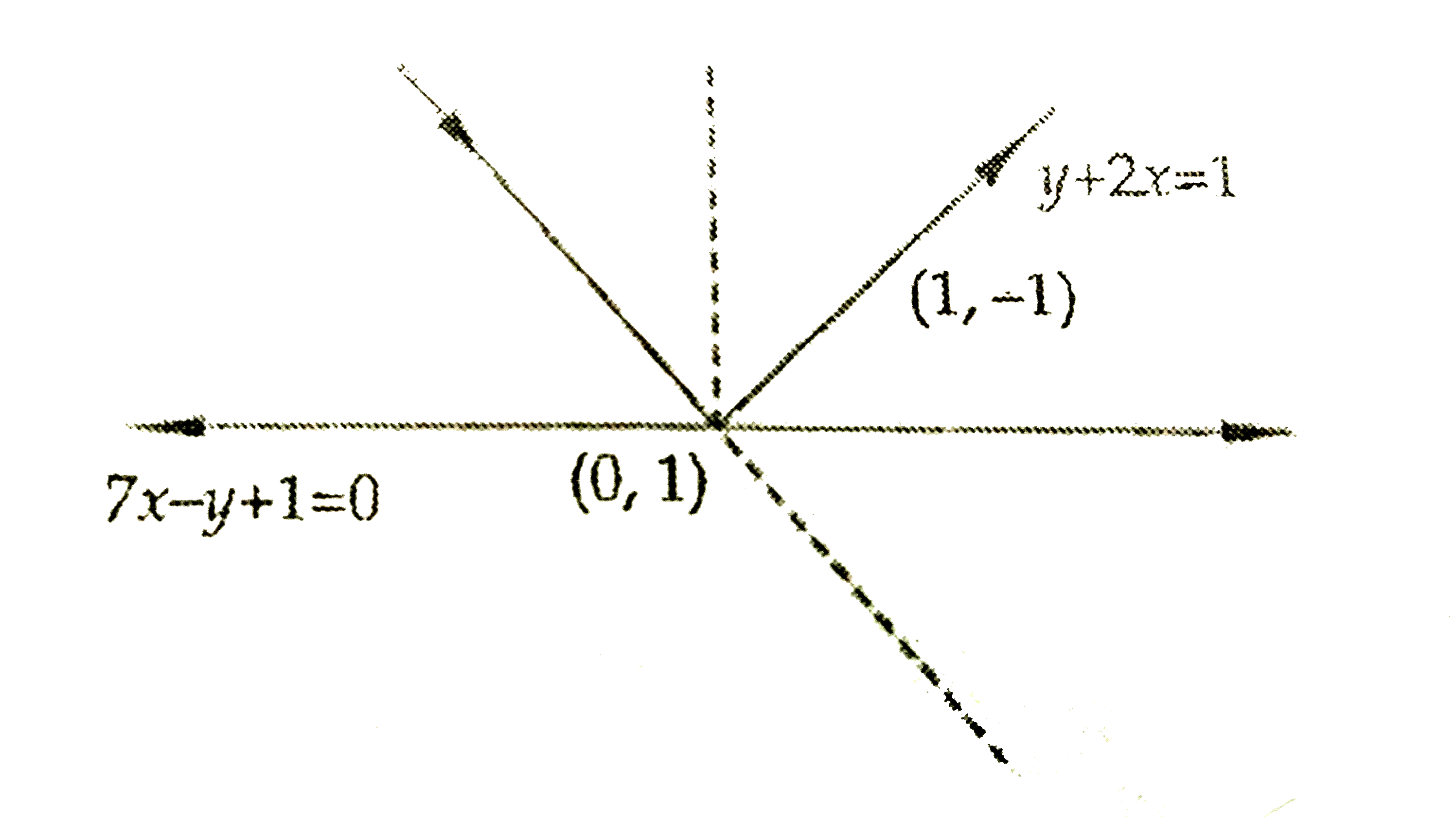
Let P(-1,1) be a point on y + 2x = 1 . The image of P(1,-1) in the line mirror 7x - y + 1 = 0 is given by
x−17=y+1−1=−2(7×1−(−1)+1)72+(−1)2
⇒x−17=y+1−1=−1850⇒x=−3825,y=−1625
The line along the incident ray i.e. equation (i) passes through (-38/25 , -16/25) .
∴7(−3825)+1625+1+λ(−7625−1625−1)=0⇒λ=−225117
Substituting the value of λ in (i) , we obtain
7x−y+1−225117(2x+y−1)=0or,41x−38y+38=0
as the line along the incident ray .
Topper's Solved these Questions
- STRAIGHT LINESBook:OBJECTIVE RD SHARMAChapter:STRAIGHT LINESExercise:Section-1 Solved MCQs (Example)
Explore 1 Video
- STRAIGHT LINESBook:OBJECTIVE RD SHARMAChapter:STRAIGHT LINESExercise:SECTION - II (ASSERTION - REASON TYPE MCQs)
Explore 14 Videos
- STRAIGHT LINESBook:OBJECTIVE RD SHARMAChapter:STRAIGHT LINESExercise:ILLUSTRATION 18
Explore 1 Video
- SETSBook:OBJECTIVE RD SHARMAChapter:SETSExercise:Chapter Test
Explore 30 Videos
Similar Questions
A ray of light is incident along a line which meets another line, 7x−y+1=0, at the point (0, 1). The ray isthen reflected from this point along the line, y+2x=1. Then the equation of the line of incidence of the ray of light is (A) 41x+38y−38=0 (B) 41x−38y+38=0 (C) 41x+25y−25=0 (D) 41x−25y+25=0
View SolutionA ray of light is sent along the line which passes through the point (2, 3). The ray is reflected from the point P on x-axis. If the reflected ray passes through the point (6, 4), then the co-ordinates of P are
View Solution
Knowledge Check
A ray travelling along the line 3x - 4y = 5 after being reflected from a line l travels along the line 5x + 12y = 13. Then, the equation of the line l is
Ax+8y= 0Bx=8yCX + 4y = 65D32x - 4y = -65Force of 1, 2 units act along the lines x=0 and y= 0, the equation of the line of acting of the resultants is
Ay−2x=0B2y−x=0Cy+x=0Dy−x=0Forces of 1 and 2units act along the lines x=0 and y=0. The equation of the line of action of the resultant is
Ay−2x=0B2y−x=0Cy+x=0Dy−x=0
A ray of light is sent along the line x−2y−3=0 upon reaching the line 3x−2y−5=0, the ray is reflected from it. Find the equation of the line containing the reflected ray.
View SolutionA ray of light is sent along the line x−2y+5=0 upon reaching the line 3x−2y+7=0 the ray is reflected from it . Find the equation of the containing the reflected ray .
View SolutionA ray of light is sent along a line x−2y−3=0 . Upon reaching the line 3x−2y−5=0 the ray is reflected. Find the equation of the line containing the reflected ray .
View SolutionIf a ray travelling the line x = 1 gets reflected the line x+y=1 then the equation of the line along which the reflected ray travels is
View SolutionThe position of reflection of the point (4,1) about the line y=x -1 is
View Solution

