Question

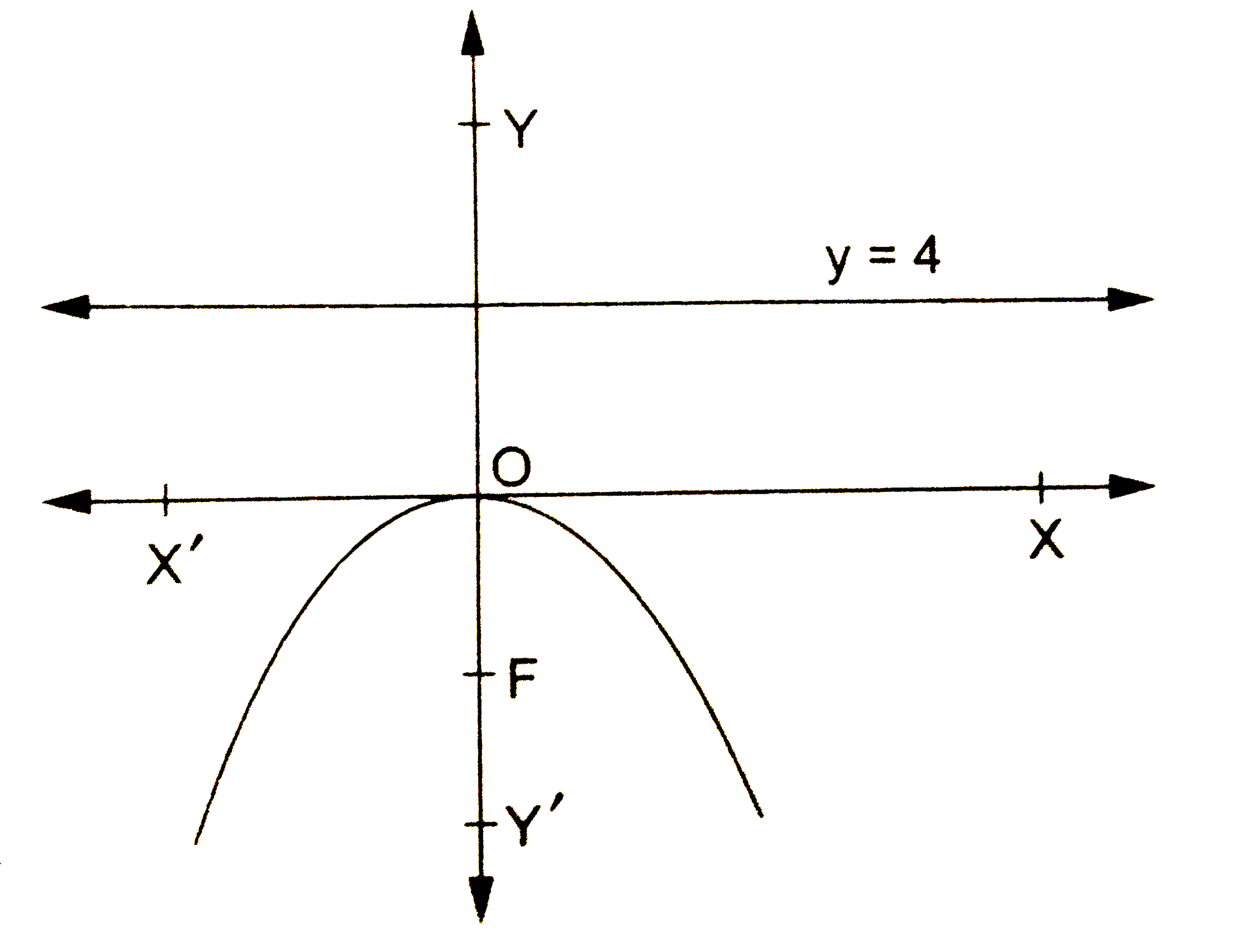
Find the coordinates of the focus and the vertex, the equations of the directix and the axis, and the lendth of the latus rectum of the parabola $x^2=-16Y$

Explanation

The given equations is of the form `x^(2)=-4ay"where "4a=16,i.e. a=4`.So, this is a case of downward parabola. Its focus is `F(0,-a),i.e. F(0,-4)` Its vertex is O(0,0). The equation of the directrix is y=a i.e, `y=4`. Its axis is y-axis, whose equations is x=0. Length of latcus rectum=`4a=(4xx4)`units=16units.