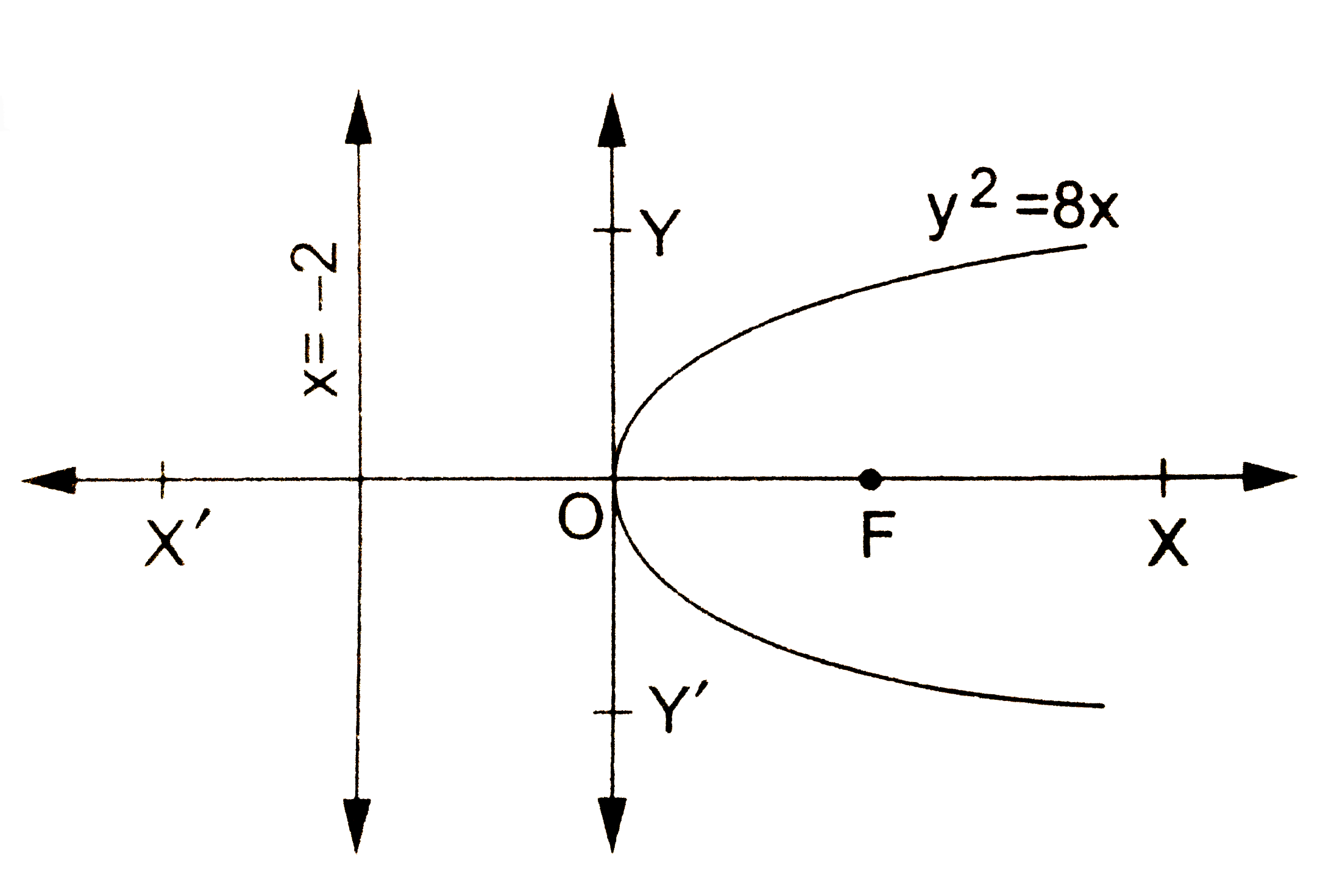
Find the coordinates of the focus and the vertex, the equations of the directix and the axis, and the lendth of the latus rectum of the parabola y2=8x
The given equations is of the form y2=4ax, where 4a=8, i.e. a=2
This is a right-handed parabola. Its focus F(a,0),ie.F(2,0) Its vertex is O(0,0). The equation of the direction is x=−a,i.e.x=−2 Its axis is x-axis, whose equation is y=0. Length of latus recum =4a=(4×2) units=8 units.
Topper's Solved these Questions
Similar Questions
Find the coordinates of the focus and the vertex, the equations of the directix and the axis, and the lendth of the latus rectum of the parabola y2=−12x
View SolutionFind the coordinates of the focus and the vertex, the equations of the directix and the axis, and the lendth of the latus rectum of the parabola x2=6y
View Solution
Knowledge Check
The length of the latus rectum of the parabola y2=8x is
A4B6C8D10The length of the latus rectum of the parabola y2=−8x will be-
A2B−8C6D4
Find the coordinates of the focus and the vertex, the equations of the directix and the axis, and the lendth of the latus rectum of the parabola x2=−16Y
View SolutionFind the coordinates of the focus and the vertex, the equations of the directrix and the axis, and length of the latus rectum of the parabola:
(i) y2=−8x (ii)y2=−6x (iii)5y2=−16x
View SolutionFind the coordinates of the focus and the vertex, the equations of the directrix and the axis, and length of the latus rectum of the parabola:
(i) y2=12x (ii) y2=10x (iii)3y2=8x
View SolutionFind the coordinates of the focus and the vertex, the equations of the directrix and the axis, and length of the latus rectum of the parabola: (i)x2=16y (ii)x2=10y (iii)3x2=8y
View SolutionFind the coordinates of the focus and the vertex, the equations of the directrix and the axis, and length of the latus rectum of the parabola:
(i)x2=−8y (ii)x2=−18y (iii)3x2=−16y
View SolutionFind the length of the latus rectum of the parabola x2=−8y.
View Solution
