If D is the mid-point of the hypotenuse AC of a right triangle ABC, prove that BD=12AC
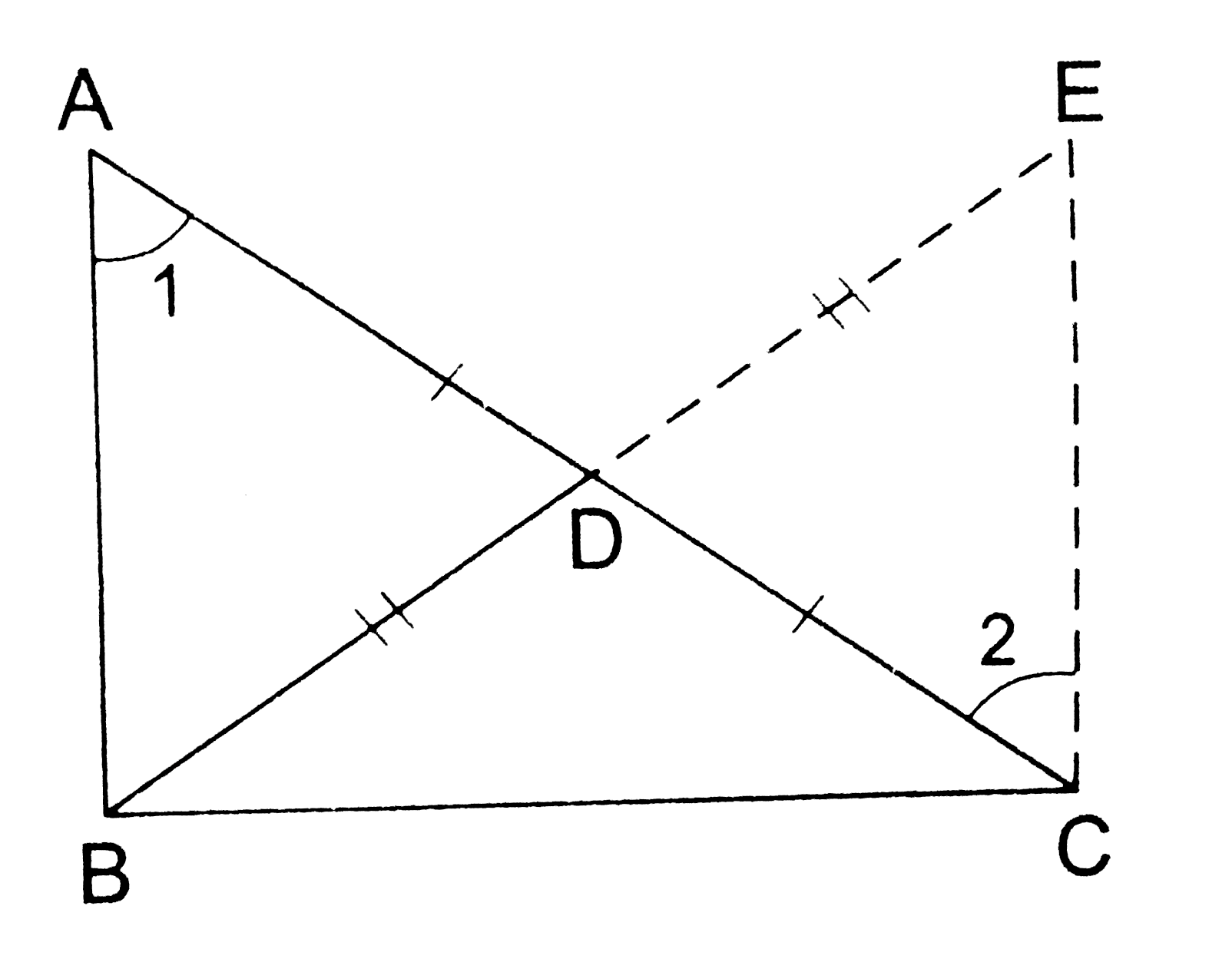
GIVEN A ΔABC in which ∠B=90∘ and D is the midpoint of aC.
TO PROVE BD=12AC.
CONSTRUCTION Produce BD to E such that BD = DE.
Join EC.
PROOF In ΔADBandΔCDE, we have
AD=CD (given)
BD=ED (by construction)
and ∠ADE=∠CDE (vert. opp. ∠s).
∴ ΔADB≅ΔCDE (SAS-criteria).
∴ AB=ECand∠1=∠2 (c.p.c.t.).
But, ∠1and∠2 are alternate interior angles.
∴ CE||BA.
Now, CE||BA and BC is the transversal.
∴ ∠ABC+∠BCE=180∘ [co. int. ∠s]
⇒ 90∘+∠BCE=180∘ [∵∠ABC=90∘]
⇒ ∠BCE=90∘
Now, inΔABCandΔECB, we have
BC=CB (common),
AB=EC (proved)
and∠CBA=∠BCE (each equal to 90∘).
∴ ΔABC≅ΔECB (SAS-criteria).
∴ AC=EB⇒12EB=12AC⇒BD=12AC.
Hence, BD=12AC.
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9A
27 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9B
16 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)
37 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
22 Videos
Similar Questions
If D is the mid-point of the hypotenuse AC of a right triangle ABC, prove that BD=12AC
View SolutionProve that the line segment joining the mid-point of the hypotenuse of a right triangle to its opposite vertex is half of the hypotenuse.
View SolutionProve that the mid-point of the hypotenuse of a right triangle is equidistant from its vertices
View SolutionIn right triangle ABC , right angle at C, M is the mid-point of the hypotenuse AB. C is jointed to M and produced to a point D such that DM=CM. Point D is joined to point B. Show that AMC≅BMD (ii) ∠DBC=90∘ (iii)DBC≅ACB (iv) CM=12AB
View SolutionIf D,E,F are the mid-points of the sides BC,CAandAB respectively of a triangle ABC, prove by vector method that AreaofDEF=14(areaofABC).
View SolutionIn right triangle ABC, right angled at C, Mis the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that

∠DBC is right angle.
View SolutionIn right triangle ABC, right angled at C, Mis the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that

ΔAMC≅ΔBMD
View SolutionIn right triangle ABC, right angled at C, Mis the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that

ΔDBC≅ΔACB
View SolutionIn right triangle ABC, right-angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see Fig. 7.23). Show that:
(i) ΔAMC≅ΔBMD
(ii) ∠DBC is a right angle
(iii) ΔDBC≅ΔACB
(iv) CM=12AB

View SolutionIf O is a point in space, ABC is a triangle and D,E,F are the mid-points of the sides BC,CA and AB respectively of the triangle, prove that →OA + →OB+→OC=→OD+→OE+→OF.
View Solution