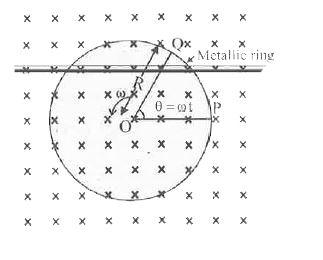
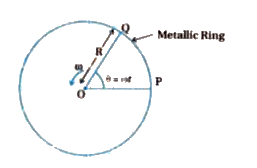
A metallic rod of 1m length is rotated with a frequency of 50 rev/s, with one end hinged at the centre and the other end at the circumference of a circular me tallic ring of radius 1m, about an axis passing through the centre and perpendicular to the plane of the ring (see figure). A constant and uniform magnetic field of 1T parallel to the axis present everywhere. What is the emf between the centre and the metallic ring?
 Solution in Tamil
Solution in Tamil
Method I
As the rod is rotated, free electrons in the rod move towards the outer end due to Lorentz force and get distributed over the ring. Thus, the resulting separation of charges produces an emf across the ends of the rod. At a certain value of emf, there is no more flow of electrons and a steady state is reached. Using Eq. (6.5), the magnitude of the emf generated across a length dr of the rod as it moves at right angles to the magnetic field is given by dε=Bvdr . Hence,
ε=∫deπs=∫R0Bvdr=∫R0Bωrdr=BωR22
Note that we have used v=ωr. This gives.
ε=12×1.0×2π×50×(12)
=157V
Method II
To calculate the emf, we can imagine a closed loop OPQ in which point O and P are connected with a resistor R and OQ is the rotating rod. The potential difference across the resistor is then equal to the induced emf and equals B x× (rate of change of area of loop). If θ is the angle between the rod and the radius of the circle at P at time t, the area of the sector OPQ is given by
πR2×θ2π=12R2θ
where R is the radius of the circle . Hence , the induced emf is
ε=B×ddt[12R2θ]=12BR2dθdt=BωR22
[Note : dθdt=ω=2πv]
This expression is identical to the expression obtained by Method I and we get the same value of ε.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT TAMILCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISES
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT TAMILCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ADDITIONAL EXERCISES
7 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - NCERT TAMILCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - EXERCISES
34 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT TAMILCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Evaluation (Numerical problems)
5 Videos
Similar Questions
Predict the direction of induced current in the situations described by the following figures (a) to (f).
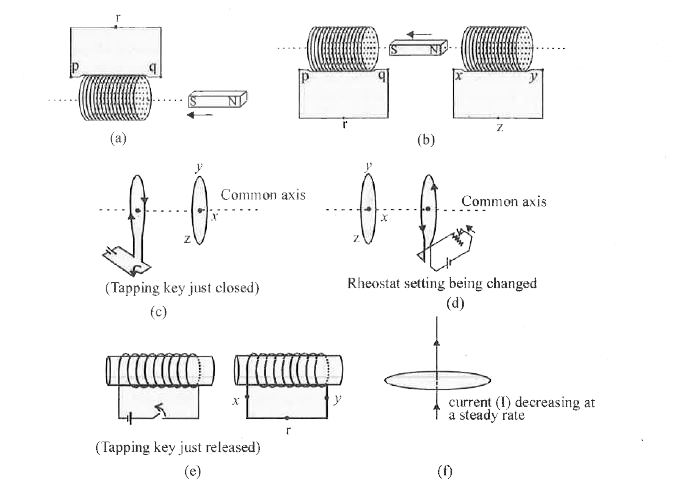
View SolutionSuppose the loop in Textual Exercise 4 is stationary but the current feeding the electromagnet that produces the magnetic field is gradually reduced so that the field decreases from its initial value of 0.3 T at the rate of 0.02Ts−1 .If the cut is joined and the loop has a resistance of 1.6Ω how much power is dissipated by the loop as heat ? What is the source of this power ?
View SolutionWhat is the force between two small charged spheres having charges of 2×10−7Cand3×10−7C placed 30cm apart in air ?
View SolutionConsider a parallel plate capacitor whose plates are closely spaced. Let R be the radius of the plates and the current in the wire connected to the plates is 5 A, calculate the displacement current through the surface passing between the plates by directly calculating the rate of change of flux of electric field through the surface.
View SolutionA metallic rod of 1 m length is rotated with a frequency of 50 rev/s, with on end hinged at the centre and the other end at the circumference of a circular metallic ring of radius 1 m, about an axis passing through the centre and perpendicular at to the plane of the ring. A constant uniform magnetic field of 1 T parallel to the axis is persent eveywhere. what is the e.m.f. between the centre and the metallic ring?
View SolutionA metallic rod of length 'I' is rotated with a frequency with one end hinged at the center and the other end at the circumference of a circular metallic ring of radius r , about an axis passing through the centre and perpendicular to the plane of the ring. A constant uniform magnetic field B parallel to the axis is present everywhere . Using Lorentz force, explain how emf is induced between the centre and the metallic ring and hence obtained the expression for it.
View Solution1 मीटर लंबी धातु की एक छड़ को 50 चक्कर/सेकंड की आवृति से घुमाया गया है | छड़ के एक सिरा वृताकार धात्विक वलय जिसकी त्रिज्या 1 मीटर है, के केंद्र पर तथा दूसरा सिरा वलय की परिधि पर कब्जे से इस प्रकार जुड़ा है कि छड़ की गति वलय के केंद्र से जाने वाले तथा वलय के ताल में अभिलंबावत अक्ष के पारित: है (चित्र 6.11) | अक्ष के अनुदिश एक स्थिर तथा एकसमान चुंबकीय क्षेत्र 1 T सर्वत्र उपस्थित है | केंद्र तथा धात्विक वलय के बिच विधुत वाहक बल क्या होगा ?

View SolutionA metallic rod of 'L' length is rotated with angular frequency of 'w' with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius L, about an axis passing through the centre and perpendicular to the plane of the ring. A constant and uniform magnetic field B parallel to the axis is present everywhere. Deduce the expression for the emf between the centre and the metallic ring.
View SolutionA metallie rod of 1 m length is rotated with a frequency of 50 revis, with one end hinged at the centre and the other end at the eireumference of a circular metallic ring of radius 1m, about an axis passing through the centre and perpendicular to the plane of the ring as in figure. A constant and uniform magnetic field of the parallel to the axis is present everywhere. What is the emf between the centre and the metallic ring?

View SolutionA metallic rod of 1m length is rotated with a frequency of 50 rev/s, with one end hinged at the centre and the other end at the circumference of a circular me tallic ring of radius 1m, about an axis passing through the centre and perpendicular to the plane of the ring (see figure). A constant and uniform magnetic field of 1T parallel to the axis present everywhere. What is the emf between the centre and the metallic ring?
View SolutionA metallic rod of 1 m length is rotated with a frequency of 50 rev/s, with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius 1 m, about an axis passing through the centre and perpendicular to the plane of the ring (Fig.). A constant and uniform magnetic field of 1 T parallel to the axis is present everywhere. What is the emf between the centre and the metallic ring?
View SolutionA metallic rod of 1 m length is rotated with a frequency of 50 rev/s, with on end hinged at the centre and the other end at the circumference of a circular metallic ring of radius 1 m, about an axis passing through the centre and perpendicular at to the plane of the ring. A constant uniform magnetic field of 1 T parallel to the axis is persent eveywhere. what is the e.m.f. between the centre and the metallic ring?
View SolutionA metallic rod of 1 m length is rotated with a frequency of 50 rev/s, with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius 1 m, about an axis passing through the centre and perpendicular to the plane of the ring as per figure. A constant and uniform magnetic field of 1T parallel to the axis is present everywhere. What is the emf between the centre and the metallic ring ?
View SolutionA metallic rod of 'L' length is rotated with angular frequency of 'w' with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius L, about an axis passing through the centre and perpendicular to the plane of the ring. A constant and uniform magnetic field B parallel to the axis is present everywhere. Deduce the expression for the emf between the centre and the metallic ring.
View SolutionA metallic rod of length 'I' is rotated with a frequency v with one end hinged at the centre and the other end at the circumference of a circualr metallic ring of a radius r, about an axis passing through the centre and perpendicular to the plane of the ring. A constant uniform magnetic field B parallel to the axis is present every where. Using Lorentz force, explain how emf is induced between the centre and the metallic ring and hence obtain the expression for it.
View SolutionA metallic rod of 1 m length is rotated with a frequency of 50 rev/s, with on end hinged at the centre and the other end at the circumference of a circular metallic ring of radius 1 m, about an axis passing through the centre and perpendicular at to the plane of the ring. A constant uniform magnetic field of 1 T parallel to the axis is persent eveywhere. what is the e.m.f. between the centre and the metallic ring?
View Solution
