Question

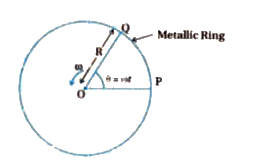
A metallie rod of 1 m length is rotated with a frequency of 50 revis, with one end hinged at the centre and the other end at the eireumference of a circular metallic ring of radius 1m, about an axis passing through the centre and perpendicular to the plane of the ring as in figure. A constant and uniform magnetic field of the parallel to the axis is present everywhere. What is the emf between the centre and the metallic ring?

Explanation

Method 1:
As the rod is rotated, free electrons in the rod move towards the outer end due to Lorentz force and get distribuled over the ring. Thus, the resulting separalion of charges produces an emi acros the ends of the rod: At a certain value of emi, there is no more flow of electrons and a steady state is reached. Using equation `(epsi=-Bl (dx)(dt)=BlV)`, the magnitude of the emf generated across a length dr of the rod as it moves at right angles to the magnetic field is given by
`depsi=Bvdr"Hence"`
`epsi=intdepsi=underset(0)overset(R)intBvdr=underset(0)overset(R)intBomegardr=(BomegaR^(2))/(2)`
Note that we have used `upsilon= omegar`. This gives
`epsi=1/2 xx 1.0 xx2pixx 50 xx (1)^(2)=157V`
Method II : To calculate the emf, we can imagine a closed loop OPQ in which point O and P are connected with a resistor R and OQ is the rotating rod. The potential difference across the resistance is then equal to the induced emf and equals `B xx` (rate of change of area of loop). If `theta` is the angle between the rod and the radius of the circle at P at time t, the area of the sector OPQ is given by
`piR^(2)xx (theta)/(2pi)=1/2R^(2)theta`
where R is the radius of the circle. Hence, the induced emf is
`piR^(2)xx (theta)/(2pi)=1/2 R^(2)theta`
`epsi=B xx (d)/(dt)[1/2 R^(2)theta]=1/2BR^(2) (d theta)/(dt)=(B omegaR^(2))/(2)`
This expression is identical to the expression obtained by Method I and we get the same value of `epsi`.