A variable circle passes through the point A(a,b) and touches the x-axis. Show that the locus of the other end of the diameter through A is (x−a)2=4by.
As shown in the figure, the variable circle passes through the point A(a,b) and touches the x-axis at ponit P.
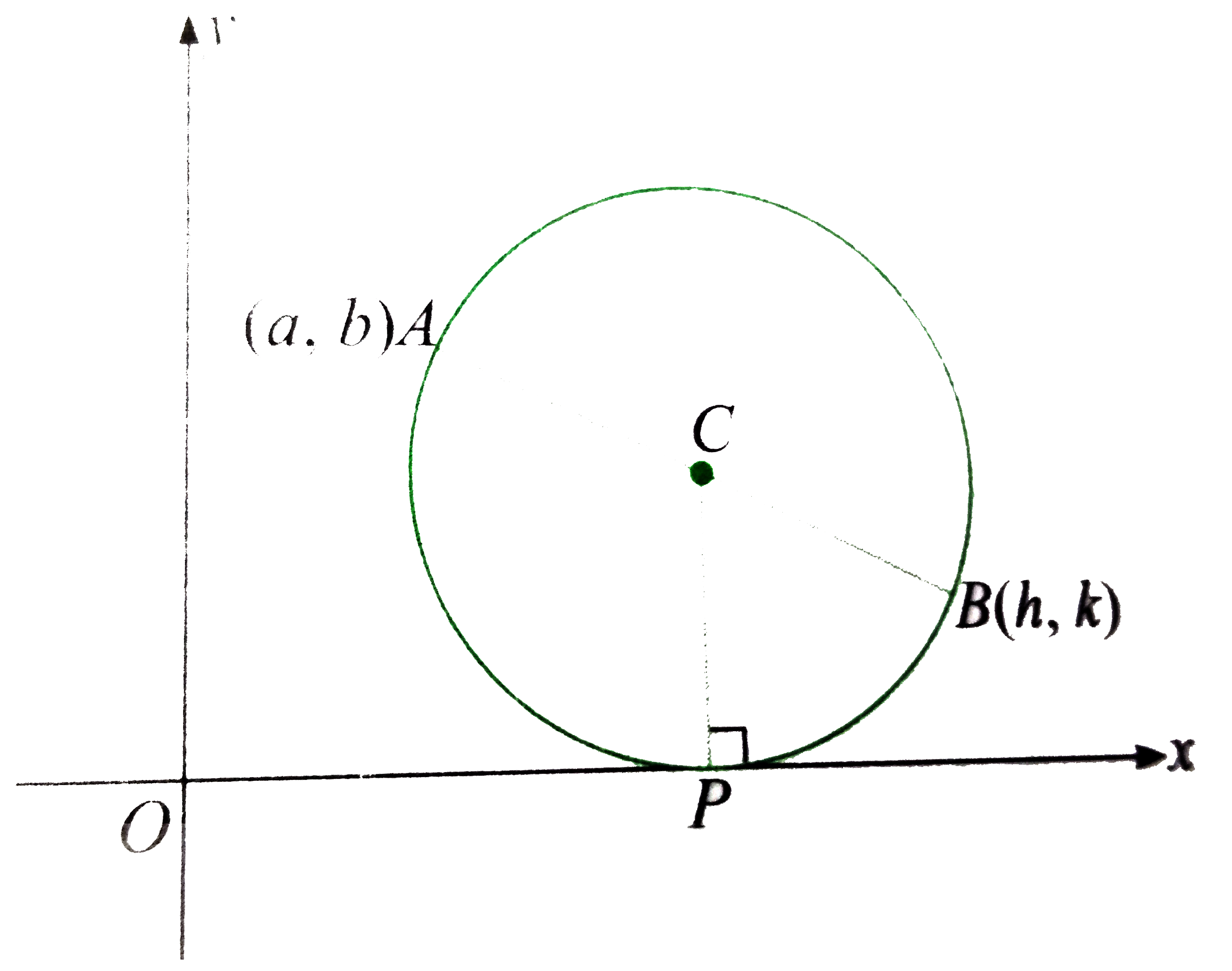
Let the other end of diameter of the circle through A be B(h,k).
So, centre of the circle is C(h+a2,k+b2)
Radius of the circle,CP=AB2
⇒∣∣∣k+b2∣∣∣=√(h−a)2+(k−b)22
Squaring and simplifying, we get (h−a)2=4bk.
Therefore, required equation of the locus is (x−a)2=4by.
Topper's Solved these Questions
- CIRCLE Book:CENGAGEChapter:CIRCLE Exercise:Exercise 4.1
Explore 14 Videos
- CIRCLE Book:CENGAGEChapter:CIRCLE Exercise:Exercise 4.2
Explore 5 Videos
- BINOMIAL THEORMBook:CENGAGEChapter:BINOMIAL THEORMExercise:Question Bank
Explore 31 Videos
- CIRCLESBook:CENGAGEChapter:CIRCLESExercise:Question Bank
Explore 32 Videos
Similar Questions
A variable circle passes through the point A(a,b) and touches the x-axis. Show that the locus of the other end of the diameter through A is (x−a)2=4by.
View SolutionA variable circle passes through the point P(1,2) and touches the x-axis. Show that the locus of the other end of the diameter through P is (x−1)2=8y.
View Solution
Knowledge Check
A variable circle passes through the fixed A(p,q) and touches the x-axis. Show that the locus of the other end of the diameter through A is (x-p)^2 = 4qy.
A(x−p)2=4qyB(x−q)2=4pyC(y−p)2=4qxD(y−q)2=4pxA variable circle passes through a fixed point A(a,b) and touches the axis of x. Locus of the other end of the diameter through A is
AcircleBparabolaCellipseDnone of theseA variable circle passes through the fixed point A(p, q) and touches x-axis. The locus of the other end of the diameter through A is:
A(y−q)2=4pxB(x−q)2=4pyC(y−p)2=4qxD(x−p)2=4qy
A variable circle passes through the fixed A(p,q) and touches the x-axis. Show that the locus of the other end of the diameter through A is (x−p)2=4qy.
View SolutionA variable circle passes through the fixed point (2, 0) and touches y-axis then the locus of its centre is
View SolutionA circle passes through A(1,1) and touches x-axis then the locus of the other end of the diameter through 'A' is
View SolutionA variable circle passes through the fixed point (2, 0) and touches y-axis Then, the locus of its centre, is
View SolutionA variable circle is described to pass through the point (a, 0) and touch the line x+y=0. Locus of the centre of the above circle is
View Solution