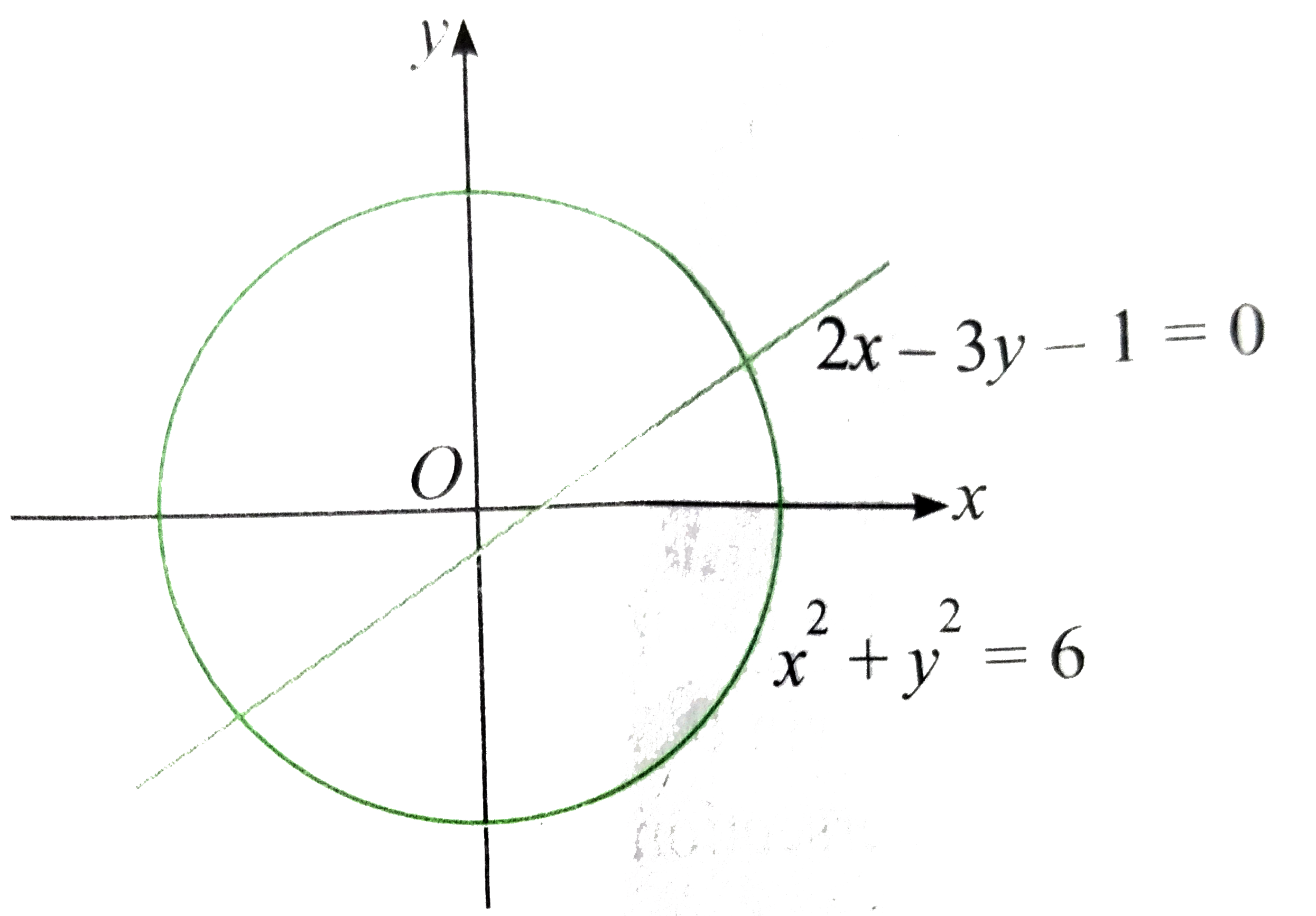
The straight line 2x-3y = 1 divides the circular region x^2+ y^2 le6 i

The d.C.s of the line 3x-1=2y-3 = 4z-1 are
A $- \frac{2}{\sqrt{61}}, \frac{3}{\sqrt{61}}, \frac{4}{\sqrt{61}}$
B $\frac{1}{\sqrt{61}}, \frac{4}{\sqrt{61}}, \frac{3}{\sqrt{61}}$
C $\frac{4}{\sqrt{61}}, \frac{6}{\sqrt{61}}, \frac{3}{\sqrt{61}}$
D $\frac{1}{\sqrt{61}}, - \frac{2}{\sqrt{61}}, \frac{3}{\sqrt{61}}$
The ration in which the plane 4x+5y-3z=8 divides the line joining the point $(- 2, 1, 5) and (3, 3, 2)$ is
A $3 : 2$
B $5 : 3$
C $1 : 4$
D $2 : 1$
Let the straight line x = b divide the area enclosed by $y = {(1 - x)}^{2}, y = 0$ and $x = 0$ into two parts $R_{1} (0 \leq x \leq b)$ and $R_{2} (b \leq x \leq 1)$ such that $R_{1} - R_{2} = \frac{1}{4}$ . Then b equals
A $\frac{3}{4}$
B $\frac{1}{2}$
C $\frac{1}{3}$
D $\frac{1}{4}$

The straight line 2x-3y = 1 divides the circular region $x^{2} + y^{2} \leq 6$ into two parts. If S = { $(2, \frac{3}{4}), (\frac{5}{2}, \frac{3}{4}), (\frac{1}{4}, - \frac{1}{4}), (\frac{1}{8}, \frac{1}{4})$ }, then the number of point(s) in S lying inside the smaller part is