A tangent PT is drawn to the circle x2+y2=4 at the point P(√3,1). A straight line L, perpendicular to PT is a tangent to the circle (x−3)2+y2=1 then find a common tangent of the two circles
x=4
y=2
x−√3y=5
x+2√2y=6
The correct Answer is:D
The point of intersection of direct common tangnets is (6,0)
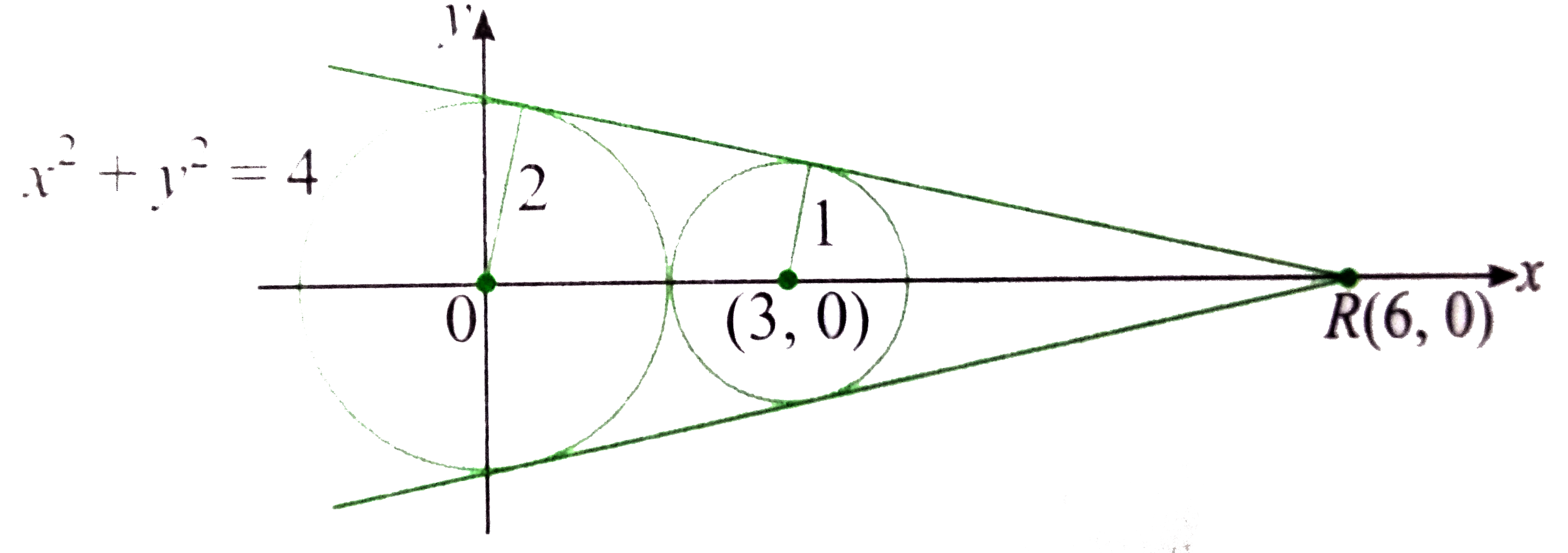
So, let the equation of common tangnet be
y−0=m(x−6)
As it touches x2+y2=4, we have
∣∣∣0−0−6m√1+m2∣∣∣=2
or 9m2=1+m2
or m=±12√2
So, the equation of common tangents are
y=12√2(x−6),y=−12√2(x−6) , also x=2
Topper's Solved these Questions
Similar Questions
A tangent PT is drawn to the circle x2+y2=4 at the point P(√3,1). A straight line L, perpendicular to PT is a tangent to the circle (x−3)2+y2=1 then find a common tangent of the two circles
View SolutionA tangent PT is drawn to the circle x2+y2=4 at the point P(√3,1). A straight line L is perpendicular to PT is a tangent to the circle (x−3)2+y2=1 Common tangent of two circle is: (A) x=4 (B) y=2 (C) x+(√3)y=4 (D) x+2(√2)y=6
View Solution
Knowledge Check
A tangent PT is drawn to the circle x2+y2=4 at the point P (√3,1). A straight line L, perpendicular to PT is a tangent to the circle (x−3)2+y2=1
a common tangent of the two circles isAx=4By=2Cx−√3y=5Dx+2√2y=6A possible equation of L is (A) x 3y 1 (B) x 3y 1 (C) x 3y 1 (D) x 3y 5
Ax−√3y=1Bx+√3y=1Cx−√3y=−1Dx+√3y=5If a line, y = mx + c is a tangent to the circle, (x−1)2+y2=1 and it is perpendicular to a line L1 , where L1 is the tangent to the circle x2+y2=8 at the point (2, 2), then :
AC2+2c−1=0Bc2−2c+1=0Cc2−2c−1=0Dc2+2c+2=0
A tangent PT is drawn to the circle x2+y2=4 at point p(√3,1) A straight line L perpendicular to PT is a tangent to the circle (x−3)2+y2=1 A possible equation of L is
View Solutionshow that the tangent of the circle x2+y2=25 at the point (3,4) and (4,-3) are perpendicular to each other.
View SolutionIf the line y=2-x is tangent to the circle S at the point P(1,1) and circle S is orthogonal to the circle x2+y2+2x+2y−2=0 then find the length of tangent drawn from the point (2,2) to the circle S
View SolutionLocus of point of intersection of perpendicular tangents to the circle x2+y2−4x−6y−1=0 is
View SolutionThe straight line 4x+3y=p is tangent to the circle x2+y2+4√3−4x−6y=0, then p equals
View Solution
